Question

17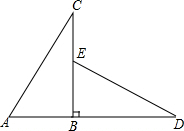．如图所示，△ABC直角三角形，延长AB到D，使BD=BC，在BC上取BE=AB，连接DE．△ABC顺时针旋转后能与△EBD重合，那么：
（1）旋转中心是哪一点？旋转角是多少度？
（2）AC与DE的关系怎样？请说明理由．

Answer 1

分析 （1）由条件易得BC和BD，BA和BE为对应边，而△ABC旋转后能与△EBD重合，于是可判断旋转中心为点B；根据旋转的性质得∠ABE等于旋转角，从而得到旋转角度；
（2）根据旋转的性质即可判断AC=DE，AC⊥DE．

解答 解：（1）∵BC=BD，BA=BE，
∴BC和BD，BA和BE为对应边，
∵△ABC旋转后能与△EBD重合，
∴旋转中心为点B；
∵∠ABC=90°，
而△ABC旋转后能与△EBD重合，
∴∠ABE等于旋转角，
∴旋转角是90度；
（2）AC=DE，AC⊥DE．理由如下：
∵△ABC绕点B顺时针旋转90°后能与△EBD重合，
∴DE=AC，DE与AC成90°的角，即AC⊥DE．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．