题目内容
解方程：
（1）x2-2x-4=0
（2）6x2-7x+1=0
（3）5x2+8-9x=0．
（1）x2-2x-4=0
（2）6x2-7x+1=0
（3）5x2+8-9x=0．
考点：解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题：
分析：（1）移项后用配方法解答；
（2）用十字相乘法解答；
（3）用公式法解答．
（2）用十字相乘法解答；
（3）用公式法解答．
解答：解：（1）移项得，x2-2x=4，
配方得，x2-2x+1=4+1，
（x-1）2=5，
x-1=±
，
x=1±
，
解得x1=1+
，x2=1-
．
（2）（6x-1）（x-1）=0，
解得x1=
，x2=1．
（3）原方程可化为5x2-9x+8=0，
a=5，b=-9，c=8，
△=81-4×5×8=-79＜0，
原方程无解．
配方得，x2-2x+1=4+1，
（x-1）2=5，
x-1=±
| 5 |
x=1±
| 5 |
解得x1=1+
| 5 |
| 5 |
（2）（6x-1）（x-1）=0，
解得x1=
| 1 |
| 6 |
（3）原方程可化为5x2-9x+8=0，
a=5，b=-9，c=8，
△=81-4×5×8=-79＜0，
原方程无解．
点评：本题考查了一元二次方程的解法，要注意不同的方程要用适当的解法．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
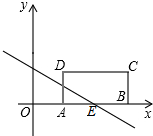如图所示，在平面直角坐标系中，矩形ABCD的边AB位于x轴，A（1，0），B（3，0），矩形的宽AD为1，一条直线y=kx+2（k≠0）与折线ABC交于点E．
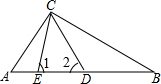如图，在△ABC中，AD=AC，BE=BC．