题目内容
因式分解：4（2y-x）+25（x-2y）3．
考点：提公因式法与公式法的综合运用
专题：
分析：首先提取公因式（2y-x），进而利用平方差公式分解因式得出即可．
解答：解：4（2y-x）+25（x-2y）3
=4（2y-x）-25（2y-x）3
=（2y-x）[4-25（2y-x）2]
=（2y-x）[4+5（2y-x）][4-5（2y-x）]
=（2y-x）（4+10y-5x）（4-10y+5x）．
=4（2y-x）-25（2y-x）3
=（2y-x）[4-25（2y-x）2]
=（2y-x）[4+5（2y-x）][4-5（2y-x）]
=（2y-x）（4+10y-5x）（4-10y+5x）．
点评：此题主要考查了提取公因式法以及公式法分解因式，熟练利用平方差公式分解因式是解题关键．
练习册系列答案
相关题目
如图，已知∠1=∠2，要说明△ABD≌△ACD还需要从下列条件中选一个，正确的说法是（ ）| A、∠B=∠C |
| B、∠ADB=∠ACD |
| C、DB=DC |
| D、AD=AD |
如图，在△ABC中，AB=AC，BE=AE，△BCE的周长为12，BC=5，求AB的长．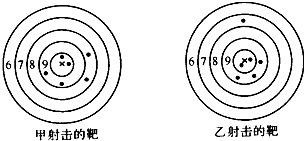
如图是甲，乙两人在一次射击比赛中靶的情况（击中靶中心的圆面为10环，靶中数字表示该数所在圆环被击中所得的环数），每人射击了6次．