Question

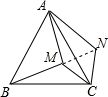
如图，M为等边△ABC内部的一点，且MA=8，MB=10，MC=6，将△BMC绕点C顺时针旋转得到△ANC．下列说法中：①MC=NC；②AM=AN；③S_{四边形AMCN}=S_△ABC﹣S_△ABM；④∠AMC=120°．正确的有__________．（请填上番号）

Answer 1

①③

【考点】全等三角形的判定与性质；等边三角形的性质．

【分析】根据旋转的性质得到CM=CN，BM=AN，故①正确，②错误；△BCM≌△ACN，于是得到S_△BCM=S_△ACN，求得S_{四边形AMCN}=S_△ACM+S_△ACN=S_△ABC﹣S_△ABM；故③正确；连接MN，根据等边三角形的性质得到∠ACB=60°，推出△CMN是等边三角形，根据等边三角形的性质得到∠CMN=60°，MN=CM=6，根据勾股定理的逆定理得到∠AMN=90°，求得∠AMC=150°，故④错误．

【解答】解：∵△BMC绕点C顺时针旋转得到△ANC，

∴CM=CN，BM=AN，故①正确，②错误；

△BCM≌△ACN，

∴S_△BCM=S_△ACN，

∴S_{四边形AMCN}=S_△ACM+S_△ACN=S_△ABC﹣S_△ABM；故③正确；

连接MN，∵△ABC是等边三角形，

∴∠ACB=60°，

∵∠ACN=∠BCM，

∴∠MCN=60°，

∴△CMN是等边三角形，

∴∠CMN=60°，MN=CM=6，

在△AMN中，∵AM²+MN²=8²+6²=10²=AN²，

∴∠AMN=90°，

∴∠AMC=150°，故④错误，

故答案为：①③．

【点评】本题考查了全等三角形的性质，旋转的性质，等边三角形的性质，勾股定理的逆定理，连接MN构造等边三角形是解题的关键．