Question

如图，在△ABC中，AB=AD=DC，∠B=60°，则∠C的度数为(     )

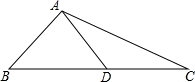
A．60°   B．30°    C．35°   D．40°

Answer 1

B【考点】等腰三角形的性质．

【分析】先根据等腰三角形的性质求出∠ADB的度数，再由平角的定义得出∠ADC的度数，根据等腰三角形的性质即可得出结论．

【解答】解：∵△ABD中，AB=AD，∠B=60°，

∴∠B=∠ADB=60°，

∴∠ADC=180°﹣∠ADB=120°，

∵AD=CD，

∴∠C=（180°﹣∠ADC）÷2=（180°﹣120°）÷2=30°，

故选：B．

【点评】本题考查的是等腰三角形的性质，熟知等腰三角形的两底角相等是解答此题的关键．