题目内容
6.(1)解不等式:$\frac{x-1}{3}$-$\frac{2x+6}{4}$>-2,并把解集在数轴上表示出来.(2)解不等式组:$\left\{\begin{array}{l}{5x-6≤2(x+3)}\\{\frac{3x}{4}-1<3-\frac{5x}{4}}\end{array}\right.$,并将不等式组的解集在所给数轴上表示出来.
分析 (1)去分母、去括号、移项、合并同类项,系数化成1即可求得不等式的解集,然后在数轴上表示即可;
(2)先求出不等式组中每一个不等式的解集,然后把不等式的解集表示在数轴上,再求出它们的公共部分就是不等式组的解集.
解答 (1)解:不等式两边乘以12得,4(x-1)-3(2x+6)>-24,
去括号,得4x-4-6x-18>-24,
移项,得4x-6x>-24+4+18,
系数化成1得:-2x>-2,
系数化1 得:x<1
不等式组的解集在数轴上表示如下: ;
;
(2)解:$\left\{\begin{array}{l}{5x-6≤2(x+3)…①}\\{\frac{3x}{4}-1<3-\frac{5x}{4}…②}\end{array}\right.$,
解不等式①得:x≤4,
解不等式②得:x<2,
不等式组的解集在数轴上表示如下: ,
,
则原不等式组的解为:x<2.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
16.方程3x-1=2x+2的解为( )
| A. | -3 | B. | -$\frac{3}{5}$ | C. | 3 | D. | -$\frac{1}{5}$ |
17.若a>b,则下列不等式一定成立的是( )
| A. | $\frac{b}{a}$<1 | B. | $\frac{b}{a}$>1 | C. | -a>-b | D. | b-a<0 |
1.已知二元一次方程2x-y=1,用y的代数式表示x为( )
| A. | x=$\frac{1+y}{2}$ | B. | x=$\frac{1-y}{2}$ | C. | y=1-2x | D. | y=2x-1 |
18.某招聘考试分笔试和面试两种,其中笔试按40%、面试按60%计算加权平均数作为总分成绩,小华笔试成绩为90分,面试成绩为85分,那么小华的总成绩是( )
| A. | 87分 | B. | 87.5分 | C. | 88分 | D. | 89分 |
 如图,在平行四边形ABCD中,AC是它的一条对角线,BE⊥AC于点E,DF⊥AC于点F,求证:四边形BEDF是平行四边形.
如图,在平行四边形ABCD中,AC是它的一条对角线,BE⊥AC于点E,DF⊥AC于点F,求证:四边形BEDF是平行四边形.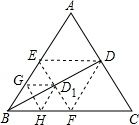 如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn=$\frac{\sqrt{3}}{{2}^{n+1}}$.
如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn=$\frac{\sqrt{3}}{{2}^{n+1}}$.