题目内容
如图,直线PR⊥⊙O的半径OB于E,PQ切⊙O于Q,BQ交直线PR于R.
(1)如图1,点E在半径OB上,求证:PR=PQ.
(2)如图2,若O与E重合,PR交⊙O于点C,A两点,当sin
∠P=
时,求tan∠C的值.
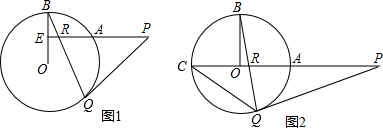
(1)如图1,点E在半径OB上,求证:PR=PQ.
(2)如图2,若O与E重合,PR交⊙O于点C,A两点,当sin
| 1 |
| 2 |
| ||
| 17 |

考点:切线的性质,解直角三角形
专题:
分析:(1)连接OQ,根据切线的性质证出∠PRQ=∠PQR,得到PQ=PR;
(2)连接AB,过O作RH⊥AB于点H,作PG⊥RQ于点G,构造直角三角形,根据三角函数的定义解答即可.
(2)连接AB,过O作RH⊥AB于点H,作PG⊥RQ于点G,构造直角三角形,根据三角函数的定义解答即可.
解答: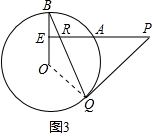 (1)证明:连接OQ,如图3,
(1)证明:连接OQ,如图3,
∵OB,OQ是⊙O的半径.
∴∠B=∠OQB,
又∵PQ为⊙O的切线,
∴∠PQB+∠OQB=90°,
又∵PE⊥OB.
∴∠B+∠ERB=∠OQB+∠PRQ,
=∠OQB+∠PQR=90°.
∴∠PRQ=∠PQR,
∴PQ=PR.
(2)连接AB,过O作RH⊥AB于点H,作PG⊥RQ于点G,如图4.
由(1)可知PQ=PR,PQ为⊙O的切线,
∴∠RPG=
∠QPR=∠OBR.
由sin
∠P=
=sin∠OBR,可以设OR=t,
则 BR=
t,OB=4t,RA=3t.
而∠BAC=
∠BOC=45°.
∴AB=4
t.
∴RH=
t=AH.BH=
t,
∴tan∠C=tan∠QBA=
=
=
.
 (1)证明:连接OQ,如图3,
(1)证明:连接OQ,如图3,∵OB,OQ是⊙O的半径.
∴∠B=∠OQB,
又∵PQ为⊙O的切线,
∴∠PQB+∠OQB=90°,
又∵PE⊥OB.
∴∠B+∠ERB=∠OQB+∠PRQ,
=∠OQB+∠PQR=90°.
∴∠PRQ=∠PQR,
∴PQ=PR.
(2)连接AB,过O作RH⊥AB于点H,作PG⊥RQ于点G,如图4.
由(1)可知PQ=PR,PQ为⊙O的切线,
∴∠RPG=
| 1 |
| 2 |

由sin
| 1 |
| 2 |
| ||
| 17 |
则 BR=
| 17 |
而∠BAC=
| 1 |
| 2 |
∴AB=4
| 2 |
∴RH=
| 3 |
| 2 |
| 2 |
| 5 |
| 2 |
| 2 |
∴tan∠C=tan∠QBA=
| RH |
| BH |
| ||||
|
| 3 |
| 5 |
点评:本题考查了切线的性质、解直角三角形,难度较大,需要做出相应的辅助线,并熟悉相关定义.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
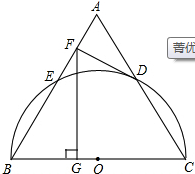 如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.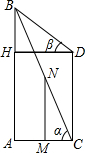 如图,在两建筑物AB、CD之间有一旗杆MN,旗杆高30米,从C点经过旗杆顶点N恰好看到建筑物AB的塔尖B点,且仰角α为60°,又从D点测得塔尖B的仰角β为45°,若旗杆底部点M为AC的中点,试分别求建筑物AB、CD的高.(结果保留根号)
如图,在两建筑物AB、CD之间有一旗杆MN,旗杆高30米,从C点经过旗杆顶点N恰好看到建筑物AB的塔尖B点,且仰角α为60°,又从D点测得塔尖B的仰角β为45°,若旗杆底部点M为AC的中点,试分别求建筑物AB、CD的高.(结果保留根号)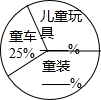 “六•一”快到了,质检部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品.图4是根据抽查结果绘制出的不完整的统计表和扇形图,请根据统计表和扇形图提供的信息,完成下列问题:
“六•一”快到了,质检部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品.图4是根据抽查结果绘制出的不完整的统计表和扇形图,请根据统计表和扇形图提供的信息,完成下列问题: