题目内容
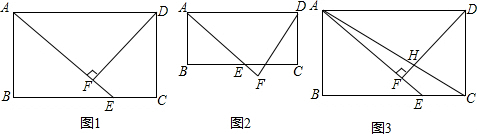
11.如图1,在矩形ABCD中,AD=12,E为BC的中点,作DF⊥AE,垂足为F.(1)求证:△ABE∽△DFA;
(2)如图2,若点F在线段AE的延长线上,求线段AB的取值范围;
(3)如图3,若F在线段AE上,DF与AC交与点H,且 $\frac{AH}{HC}$=$\frac{18}{11}$,求线段AB的长.
分析 (1)根据两角对应相等的两个三角形相似即可证明.
(2)由△ABE∽△DFA得到$\frac{12}{AE}$=$\frac{AF}{6}$,AF=$\frac{72}{AE}$,求出AE=AF时,AB的值即可解决问题.
(3)由△ADH∽△CHM得到$\frac{AH}{HC}$=$\frac{AD}{MC}$=$\frac{18}{11}$,求出CM、ME,设AB=a,则有AE=$\sqrt{36+{a}^{2}}$,EF=$\frac{1}{10}$$\sqrt{36+{a}^{2}}$,由△MFE∽△ABE列出方程即可解决.
解答 (1)证明:如图1中,
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC
∵DF⊥AE∴∠AFD=∠B=90°,
∵AD∥BC∴∠DAF=∠BEA,
∴△ABE∽△DFA.
(2)如图2中,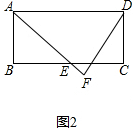
解:∵△ABE∽△DFA
∴$\frac{12}{AE}$=$\frac{AF}{6}$,AF=$\frac{72}{AE}$,
当AF=AE=6$\sqrt{2}$时△ABE和△DCE为等腰直角三角形,可得AB=6.
当点F在线段AE的延长线时0<AB<6.
(3)如图3中,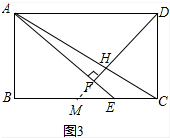
当AB>6时,延长DF交BC于点M
∵AD∥BC∴△ADH∽△CHM
∴$\frac{AH}{HC}$=$\frac{AD}{MC}$=$\frac{18}{11}$,
∴CM=$\frac{22}{3}$,则有ME=$\frac{4}{3}$,
∵AD∥ME
∴△ADF∽△EMF
∴$\frac{AF}{EF}$=$\frac{AD}{ME}$=$\frac{9}{1}$,
设AB=a,则有AE=$\sqrt{36+{a}^{2}}$,EF=$\frac{1}{10}$$\sqrt{36+{a}^{2}}$,
∵∠FEM=∠AEB,∠MFE=∠B=90°
∴△MFE∽△ABE,
∴$\frac{ME}{AE}$=$\frac{EF}{BE}$
∴$\frac{\frac{4}{3}}{\sqrt{36+{a}^{2}}}$=$\frac{\frac{1}{10}\sqrt{36+{a}^{2}}}{6}$,
∴a2+36=80,
∴a=2$\sqrt{11}$,即AB=2$\sqrt{11}$,
点评 本题考查相似三角形的判定和性质、矩形的性质、平行线的性质、勾股定理等知识,解题的关键是灵活运用相似三角形的判定和性质解决问题,把问题转化为方程解决,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | 3a+2b=5ab | B. | 2a3+3a2=5a5 | C. | 5a2-4a2=1 | D. | 5a2b-5ba2=0 |
| 居民(户) | 5 | 3 | 3 | 4 |
| 月用电量(度/户) | 30 | 42 | 50 | 51 |
| A. | 平均数是43.25 | B. | 众数是30 | C. | 方差是82.4 | D. | 中位数是42 |
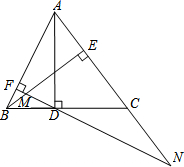 如图,AD、BE是△ABC的两条高,过点D作DF⊥AB,垂足为F,FD交BE于M,FD、AC的延长线交于点N.
如图,AD、BE是△ABC的两条高,过点D作DF⊥AB,垂足为F,FD交BE于M,FD、AC的延长线交于点N. 如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=-$\frac{3}{4}$x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=-$\frac{3}{4}$x+b与圆相切于点M,分别交x轴、y轴于B、C两点. 如图,点C是AB为直径的半圆上一点(O为圆心),以AC、BC为边向上作正方形ACDE和正方形ECFG,点P是DF的中点,若OP=6$\sqrt{2}$,AB=10,则△ABC的面积为多少?
如图,点C是AB为直径的半圆上一点(O为圆心),以AC、BC为边向上作正方形ACDE和正方形ECFG,点P是DF的中点,若OP=6$\sqrt{2}$,AB=10,则△ABC的面积为多少?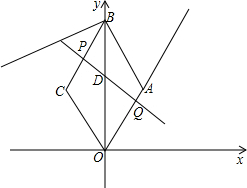 已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8$\sqrt{3}$),点P从点C开始以每秒1个单位长度的速度沿线段CB向点B移动,同时,点Q从点O开始以每秒3个单位长度的速度沿射线OA方向移动,点P运动到点B时,两点停止运动.直线PQ交OB于点D,运动时间为t秒.
已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,8$\sqrt{3}$),点P从点C开始以每秒1个单位长度的速度沿线段CB向点B移动,同时,点Q从点O开始以每秒3个单位长度的速度沿射线OA方向移动,点P运动到点B时,两点停止运动.直线PQ交OB于点D,运动时间为t秒.