题目内容
16. 如图,点C是AB为直径的半圆上一点(O为圆心),以AC、BC为边向上作正方形ACDE和正方形ECFG,点P是DF的中点,若OP=6$\sqrt{2}$,AB=10,则△ABC的面积为多少?
如图,点C是AB为直径的半圆上一点(O为圆心),以AC、BC为边向上作正方形ACDE和正方形ECFG,点P是DF的中点,若OP=6$\sqrt{2}$,AB=10,则△ABC的面积为多少?
分析 连接AD、BF,设AC=a,BC=b,首先证明AD+BF=2OP,得a+b=12,再根据a2+b2=100求出$\frac{1}{2}$ab即可解决问题.
解答 解: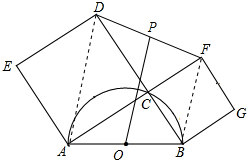 如图,连接AD、BF.设AC=a,BC=b,
如图,连接AD、BF.设AC=a,BC=b,
∵AB是直径,
∴∠ACB=90°
∵四边形ACDE、四边形BCFG都是正方形,
∴∠ACD=∠BCF=∠ACB=90°,
∴A、C、F共线,B、C、D共线,
∴∠DAC=∠BFC=45°,
∴AD∥BF,
∵DP=PF,AO=OB,
∴AD+BF=2PO,
∴$\sqrt{2}$a+$\sqrt{2}$b=12$\sqrt{2}$,
∴a+b=12,
又∵a2+b2=100,
∴a2+2ab+b2=144,
∴2ab=44,
∴S△ABC=$\frac{1}{2}$ab=11.
点评 本题考查正方形的性质、图象中位线定理,勾股定理等知识,解题的关键是添加辅助线,构造梯形,利用梯形中位线解决问题,属于中考常考题型.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
6.a6÷a3结果是( )
| A. | a3 | B. | a2 | C. | a9 | D. | a-3 |
7.下列计算中,正确的是( )
| A. | -a(3a2-1)=-3a3-a | B. | (-2a-3)(2a-3)=9-4a2 | ||
| C. | (2+x)(x-2)=4-x2 | D. | (ab-c)(-c+ab)=a2b2-c2 |
1.下列计算正确的是( )
| A. | b5•b5=2b5 | B. | (an-1)3=a3n-1 | C. | a+2a2=3a3 | D. | (a-b)5(b-a)4=(a-b)9 |
8.(-x4)3等于( )
| A. | x7 | B. | x12 | C. | -x7 | D. | -x12 |
6.下列运算正确的是( )
| A. | (-a3)2=-a6 | B. | a8÷a4=a2 | C. | (a-b)2=a2-b2 | D. | a2•a3=a5 |
 如图,△ABC的边BC长是8,BC边上的高AD′是4,点D在BC运动,设BD长为x,请写出△ACD的面积y与x之间的函数关系式y=-2x+16.
如图,△ABC的边BC长是8,BC边上的高AD′是4,点D在BC运动,设BD长为x,请写出△ACD的面积y与x之间的函数关系式y=-2x+16.