题目内容
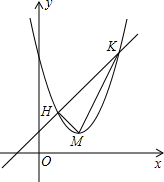 如图,抛物线y=x2-4x+5顶点为M,平移直线y=x交抛物线于点H、K,若S△MHK=3,求平移后直线的解析式.
如图,抛物线y=x2-4x+5顶点为M,平移直线y=x交抛物线于点H、K,若S△MHK=3,求平移后直线的解析式.考点:二次函数图象与几何变换
专题:几何变换
分析:设平移后的直线解析式为y=x+b,利用配方法确定对称轴为直线x=2,顶点M的坐标为(2,1),直线y=x+b与直线x=2交于P点,则P(2,2+b);设H、K的横坐标分别为a,b,则a、b为方程x2-4x+5=x+b的解,利用根与系数的关系得到b-a=
,把△MHK的面积分为△PMK和△PMH的面积和,它们的底边都是PM,高的和为b-a,则S△MHK=
•PM•(b-a)=3,所以(b+1)•
=6,解得b=1,于是得到平移后的直线解析式为y=x+1.
| 4b+5 |
| 1 |
| 2 |
| 4b+5 |
解答:解:设平移后的直线解析式为y=x+b,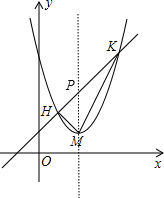
y=x2-4x+5=(x-2)2+1,
所以抛物线的对称轴为直线x=2,顶点M的坐标为(2,1),
直线y=x+b与直线x=2交于P点,则P(2,2+b),
设H、K的横坐标分别为a,b,则a、b为方程x2-4x+5=x+b的解,
所以b-a=
=
=
,
所以S△MHK=
•PM•(b-a)=3,
即(b+1)•
=6,
解得b=1.
所以平移后的直线解析式为y=x+1.

y=x2-4x+5=(x-2)2+1,
所以抛物线的对称轴为直线x=2,顶点M的坐标为(2,1),
直线y=x+b与直线x=2交于P点,则P(2,2+b),
设H、K的横坐标分别为a,b,则a、b为方程x2-4x+5=x+b的解,
所以b-a=
| (b+a)2-4ab |
| 52-4(5-b) |
| 4b+5 |
所以S△MHK=
| 1 |
| 2 |
即(b+1)•
| 4b+5 |
解得b=1.
所以平移后的直线解析式为y=x+1.
点评:本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
2013年12月15日,“玉兔号”月球车月面软着陆后离地球380000千米,能够看到地球等离子层的全貌.380000千米用科学记数法表示为( )
| A、38×107米 |
| B、3.8×108米 |
| C、3.8×109米 |
| D、0.38×109米 |
下列说法不正确的是( )
| A、一组邻边相等的矩形是正方形 |
| B、对角线相等的菱形是正方形 |
| C、对角线互相垂直的矩形是正方形 |
| D、对角线互相垂直且相等的四边形是正方形 |
 如图,OB是∠AOC的平分线,∠BOC=30°,∠COD=40°,求∠AOD的度数.
如图,OB是∠AOC的平分线,∠BOC=30°,∠COD=40°,求∠AOD的度数. 如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.
如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.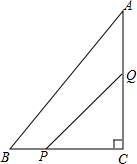 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,一动点P从点B出发,沿BC方向以1cm/s的速度向C移动,另一动点Q从点C出发,沿CA方向以2cm/s的速度向点A移动,点P、Q同时开始移动多少时间后,△CPQ与△CAB相似?
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,一动点P从点B出发,沿BC方向以1cm/s的速度向C移动,另一动点Q从点C出发,沿CA方向以2cm/s的速度向点A移动,点P、Q同时开始移动多少时间后,△CPQ与△CAB相似? 如图,AB、CD是⊙O的直径,弦DE∥AB,连接AE、AC.求证:AE=AC.
如图,AB、CD是⊙O的直径,弦DE∥AB,连接AE、AC.求证:AE=AC.