题目内容
19.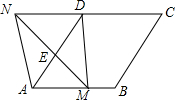 如图,在菱形ABCD中,AB=2,∠DAB=60°,点E时AD边的中点,点M时AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E时AD边的中点,点M时AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.(1)求证:四边形AMDN是平行四边形.
(2)填空:①当AM的值为1时,四边形AMDN是矩形;
②当AM的值为2时,四边形AMDN是菱形.
分析 (1)根据菱形的性质可得ND∥AM,再根据两直线平行,内错角相等可得∠NDE=∠MAE,∠DNE=∠AME,根据中点的定义求出DE=AE,然后利用“角角边”证明△NDE和△MAE全等,根据全等三角形对应边相等得到ND=MA,然后利用一组对边平行且相等的四边形是平行四边形证明;
(2)①根据矩形的性质得到DM⊥AB,再求出∠ADM=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半,即可得出结果;
②根据菱形的性质得到AN=DN,证得△ADN为等边三角形,即可得出结果.
解答 (1)证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
∵点E是AD中点,
∴DE=AE,
在△NDE和△MAE中,
$\left\{\begin{array}{l}{∠NDE=∠MAE}\\{∠DNE=∠AME}\\{DE=AE}\end{array}\right.$,
∴△NDE≌△MAE(AAS),
∴ND=MA,
∴四边形AMDN是平行四边形;
(2)①AM=1时,四边形AMDN是矩形;理由如下:
∵四边形ABCD是菱形,
∴AD=AB=2,
∵平行四边形AMDN是矩形,
∴DM⊥AB,
即∠DMA=90°,
∵∠DAB=60°,
∴∠ADM=30°,
∴AM=$\frac{1}{2}$AD=1;
②当AM=2时,四边形AMDN是菱形;理由如下:
∵四边形ABCD是菱形,
∴AD=AB=2,
∵平行四边形AMDN是菱形,
∴AN=DN,
∵∠DAB=60°,
∴∠ADN=60°,
∴△ADN为等边三角形,
∴AM=DN=AD=2.
点评 本题考查了菱形的性质、平行四边形的判定、全等三角形的判定与性质、矩形的性质、等边三角形的判定与性质等知识;熟练掌握三角形全等与证明等边三角形是解决问题的关键.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案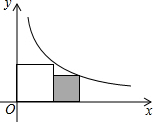 如图摆放的两个正方形,各有一个顶点在反比例函数y=$\frac{4}{x}$的图象上,则图中小正方形(阴影部分)的边长等于( )
如图摆放的两个正方形,各有一个顶点在反比例函数y=$\frac{4}{x}$的图象上,则图中小正方形(阴影部分)的边长等于( )| A. | $\sqrt{5}$-1 | B. | $\sqrt{5}$-2 | C. | 1+$\sqrt{5}$ | D. | 4-$\sqrt{5}$ |
 如图,E是?ABCD内任一点,若S?ABCD=8,则阴影部分的面积是( )
如图,E是?ABCD内任一点,若S?ABCD=8,则阴影部分的面积是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
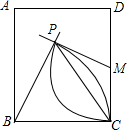 如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( )
如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( )| A. | 55° | B. | 40° | C. | 35° | D. | 20° |