题目内容
13. 如图,已知矩形ABCD,AB=3,BC=4,点P是边AD的上一点,将△ABP沿着直线BP翻折,点A的对应点为点A′.若点A′到B点的距离等于它到CD边的距离,则AP=9-6$\sqrt{2}$.
如图,已知矩形ABCD,AB=3,BC=4,点P是边AD的上一点,将△ABP沿着直线BP翻折,点A的对应点为点A′.若点A′到B点的距离等于它到CD边的距离,则AP=9-6$\sqrt{2}$.
分析 根据折叠的性质得到A′B=AB=3,AP=A′P,当点A′到直线CD的距离等于A′B的长时,过点A′作EF⊥AD垂足为E,交BC于F.得到A′B=DE=CF=3=CD,根据勾股定理得到A′F=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,EA1=3-2$\sqrt{2}$,得到AP=A′P=1-PE,根据勾股定理列方程即可得到结论.
解答  解:∵将△ABP沿着直线BP翻折,点A的对应点为点A′,
解:∵将△ABP沿着直线BP翻折,点A的对应点为点A′,
∴A′B=AB=3,AP=A′P,
∴点A′到直线CD的距离等于A′B的长时,过点A′作EF⊥AD垂足为E,交BC于F.
∴A′B=DE=CF=3=CD,
在Rt△BFA′中,BF=1,BA′=3,
∴A′F=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,EA1=3-2$\sqrt{2}$,
∵AE=1,
∴AP=A′P=1-PE,
∵A′P2=PE2+A′E2,
∴(1-PE)2=PE2+(3-2$\sqrt{2}$)2,
∴PE=6$\sqrt{2}$-8,
∴AP=9-6$\sqrt{2}$,
故答案为:9-6$\sqrt{2}$.
点评 本题考查了翻折变换-折叠问题,矩形的性质,正方形的判定和性质,勾股定理,正确的作出图形是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
2.若$\sqrt{x-\frac{1}{8}}$+$\sqrt{\frac{1}{8}-x}$有意义,则$\root{3}{x}$=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{8}$ |
 如图,矩形ABCD中,CE平分∠BCD,∠ACE=15°,则∠DOC,∠BOE的度数分别是30°和75°.
如图,矩形ABCD中,CE平分∠BCD,∠ACE=15°,则∠DOC,∠BOE的度数分别是30°和75°.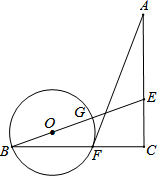 如图,AC=BC,∠C=90°,点E在AC上,点F在BC上,且CE=CF.连结AF和BE上,⊙O经过点B、F.
如图,AC=BC,∠C=90°,点E在AC上,点F在BC上,且CE=CF.连结AF和BE上,⊙O经过点B、F. 己知A(-1,0),B(2,0),点P是直线y=x+4上的一动点且在x轴上方,如果以点A、B、P、Q为顶点的平行四边形的面积等于6,画出图形并求出点P和点Q的坐标.
己知A(-1,0),B(2,0),点P是直线y=x+4上的一动点且在x轴上方,如果以点A、B、P、Q为顶点的平行四边形的面积等于6,画出图形并求出点P和点Q的坐标.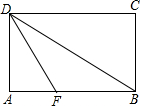 如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在BD的中点处,则∠ADF=30°.
如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在BD的中点处,则∠ADF=30°. 如图,菱形ABCD中,P为AB中点,∠A=60°,折叠菱形ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC的大小为75°.
如图,菱形ABCD中,P为AB中点,∠A=60°,折叠菱形ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC的大小为75°.