题目内容
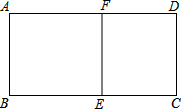如图所示，在矩形ABCD中，AB=6cm，BC=8cm，过点E作直线EF垂直于BC，将矩形ABCD分为两个矩形，使得其中一个矩形与原矩形相似，则这样的点E的个数为考点：相似多边形的性质
专题：常规题型
分析：设BE=x，则CE=8-x，分类讨论：当矩形ABEF与矩形ABCD相似，根据相似的性质得
=
，可求得x=
；当矩形CDER与矩形ABCD相似时，根据相似的性质得
=
，可求得x=
．
| 6 |
| x |
| 8 |
| 6 |
| 9 |
| 2 |
| 6 |
| 8-x |
| 8 |
| 6 |
| 7 |
| 2 |
解答：解：设BE=x，则CE=8-x，
当矩形ABEF与矩形ABCD相似，则
=
，即
=
，解得x=
；
当矩形CDER与矩形ABCD相似时，则
=
，即
=
，解得x=
，
综上所述，当BE为
或
时，将矩形ABCD分为两个矩形，其中一个矩形与原矩形相似．
故答案为2．
当矩形ABEF与矩形ABCD相似，则
| AB |
| BE |
| BC |
| AB |
| 6 |
| x |
| 8 |
| 6 |
| 9 |
| 2 |
当矩形CDER与矩形ABCD相似时，则
| AB |
| EC |
| BC |
| AB |
| 6 |
| 8-x |
| 8 |
| 6 |
| 7 |
| 2 |
综上所述，当BE为
| 7 |
| 2 |
| 9 |
| 2 |
故答案为2．
点评：本题考查了相似多边形的性质：对应角相等；对应边的比相等．也考查了矩形的性质．
练习册系列答案
相关题目
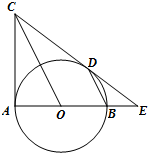如图，已知AB为⊙O的直径，AC为⊙O的切线，连结CO．BD∥OC交⊙O于D，延长AB、CD交于点E．