题目内容
喝粥牡丹砖雕艺术节于5月3日在临夏市东郊 公园隆重举行,某商贩决定在此艺术节期间经销一种艺术品,一种这种艺术品的成本价为每件20元,经市场调查发现,该艺术品每天的销售量y(件)与销售价x(元/件)之间的关系为y=-2x+80,设这种艺术品每天的销售利润为p元.
(1)求p与x之间的函数关系式;
(2)该艺术品的销售价定为每件多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种艺术品的销售价不高于每件28元,该商贩想要每天获得150元的销售利润,销售价应定为每件多少元?
(1)求p与x之间的函数关系式;
(2)该艺术品的销售价定为每件多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种艺术品的销售价不高于每件28元,该商贩想要每天获得150元的销售利润,销售价应定为每件多少元?
考点:二次函数的应用
专题:应用题
分析:(1)用每件的利润(x-20)乘以销售量即可得到每天的销售利润,即p=(x-20)y=(x-20)(-2x+80),然后化为一般式即可;
(2)把(1)中的解析式进行配方得到顶点式y=-2(x-30)2+200,然后根据二次函数的最值问题求解;
(3)求函数值为150所对应的自变量的值,即解方程-2(x-30)2+200=150,然后利用销售价不高于每件28元确定x的值.
(2)把(1)中的解析式进行配方得到顶点式y=-2(x-30)2+200,然后根据二次函数的最值问题求解;
(3)求函数值为150所对应的自变量的值,即解方程-2(x-30)2+200=150,然后利用销售价不高于每件28元确定x的值.
解答:解:(1)p=(x-20)y
=(x-20)(-2x+80)
=-2x2+120x-1600(20≤x≤40);
(2)y=-2(x-30)2+200,
因为a=-2<0,
所以x=30时,y的最大值为200,
即销售价定为每件30元时,每天的销售利润最大,最大利润是200元;
(3)当y=150时,-2(x-30)2+200=150,解得x1=35,x2=25,
而销售价不高于每件28元,
所以x=25,
即商贩想要每天获得150元的销售利润,销售价应定为每件25元.
=(x-20)(-2x+80)
=-2x2+120x-1600(20≤x≤40);
(2)y=-2(x-30)2+200,
因为a=-2<0,
所以x=30时,y的最大值为200,
即销售价定为每件30元时,每天的销售利润最大,最大利润是200元;
(3)当y=150时,-2(x-30)2+200=150,解得x1=35,x2=25,
而销售价不高于每件28元,
所以x=25,
即商贩想要每天获得150元的销售利润,销售价应定为每件25元.
点评:本题考查了二次函数的实际应用:利用二次函数解决利润问题,在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.

练习册系列答案
相关题目
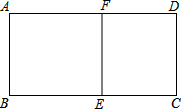 如图所示,在矩形ABCD中,AB=6cm,BC=8cm,过点E作直线EF垂直于BC,将矩形ABCD分为两个矩形,使得其中一个矩形与原矩形相似,则这样的点E的个数为
如图所示,在矩形ABCD中,AB=6cm,BC=8cm,过点E作直线EF垂直于BC,将矩形ABCD分为两个矩形,使得其中一个矩形与原矩形相似,则这样的点E的个数为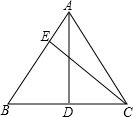 如图,在△ABC中,AB=AC=6,BD=CD=4,CE⊥AB于点E,求线段BE的长.
如图,在△ABC中,AB=AC=6,BD=CD=4,CE⊥AB于点E,求线段BE的长.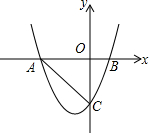 抛物线y=x2+x-2交x轴于点A、B,交y轴于点C,
抛物线y=x2+x-2交x轴于点A、B,交y轴于点C, 在等边△ABC中,D是AC中点,E为BC延长线一点,且DB=DE,求证:△DCE是等腰三角形.
在等边△ABC中,D是AC中点,E为BC延长线一点,且DB=DE,求证:△DCE是等腰三角形.