题目内容
3．下列式子正确的是（ ）| A． | sin55°＜cos36° | B． | sin55°＞cos36° | C． | sin55°=cos36° | D． | sin55°+cos36°=1 |
分析 先把余弦函数化为正弦函数得到cos36°=sin54°，而根据当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小），所以sin55°＞sin54°，于是得到sin55°＞cos36°．
解答 解：∵cos36°=cos（90°-54°）=sin54°，
而sin55°＞sin54°，
∴sin55°＞cos36°．
故选B．
点评 本题考查了锐角三角函数的增减性：锐角三角函数值都是正值，当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）；余弦值随着角度的增大（或减小）而减小（或增大）；正切值随着角度的增大（或减小）而增大（或减小）．也考查了互余公式．
练习册系列答案
天天练口算系列答案
相关题目
8．下表是二次函数y=ax2+bx+c（ a≠0）图象上部分点的横坐标（x）和纵坐标（y）．
（1）观察表格，直接写出m=3；
（2）其中A（x1，y1）、B（x2，y2）在函数的图象上，且-1＜x1＜0，2＜x2＜3，则y1＞y2（用“＞”或“＜”填空）；
（3）求这个二次函数的表达式．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | m | 8 | … |
（2）其中A（x1，y1）、B（x2，y2）在函数的图象上，且-1＜x1＜0，2＜x2＜3，则y1＞y2（用“＞”或“＜”填空）；
（3）求这个二次函数的表达式．
如图，抛物线y=x2-2x-3交x轴于A（-1，0）、B（3，0），交y轴于C（0，-3），M是抛物线的顶点，现将抛物线沿平行于y轴的方向向上平移三个单位，则曲线CMB在平移过程中扫过的面积为9（面积单位）．
如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE，若∠CAE=65°，∠E=70°，且AD⊥BC，则∠BAC的度数为85°．
如图，P为等边△ABC内一点，PA=2，PB=1，PC=$\sqrt{3}$，则△ABC的面积为$\frac{7\sqrt{3}}{4}$．
13．
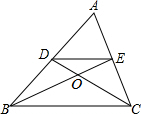如图，在△ABC中两条中线BE、CD相交于点O，记△DOE的面积为S1，△COB的面积为S2，则S1：S2=（ ）
如图，在△ABC中两条中线BE、CD相交于点O，记△DOE的面积为S1，△COB的面积为S2，则S1：S2=（ ）| A． | 1：4 | B． | 2：3 | C． | 1：3 | D． | 1：2 |