如图.将△ABC绕点A逆时针旋转一定角度.得到△ADE.若∠CAE=65°.∠E=70°.且AD⊥BC.则∠BAC的度数为85°．题目和参考答案——青夏教育精英家教网—

题目内容

8．

如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE，若∠CAE=65°，∠E=70°，且AD⊥BC，则∠BAC的度数为85°．

分析先根据旋转的性质得∠BAD=∠CAE=65°，∠C=∠E=70°，再利用互余计算出∠DAC=90°-∠C=20°，然后计算∠BAD+∠DAC即可．

解答解：∵△ABC绕点A逆时针旋转一定角度，得到△ADE，
∴∠BAD=∠CAE=65°，∠C=∠E=70°，
∵AD⊥BC，
∴∠DAC=90°-∠C=20°，
∴∠BAC=∠BAD+∠DAC=65°+20°=85°．
故答案为85°．

点评本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．

练习册系列答案

	A．	抛物线与x轴有两个交点		B．	当x=1时，函数有最大值
	C．	抛物线可由$y=-\frac{1}{2}{x^2}$经过平移得到		D．	当-1＜x≤2时，函数y的整数值有3个

13．解方程：$\frac{x}{x-1}$-2=$\frac{3}{1-x}$．

2a³+3a²=5a⁵

13．已知等腰直角△ABC中，∠BAC=90°，AB=AC=2，动点P在直线BC上运动（不与点B、C重合）．
（1）如图1，点P在线段BC上，作∠APQ=45°，PQ交AC于点Q．
①求证：△ABP∽△PCQ；②当△APQ是等腰三角形时，求AQ的长．
（2）①如图2，点P在BC的延长线上，作∠APQ=45°，PQ的反向延长线与AC的延长线相交于点D，是否存在点P，使△APD是等腰三角形？若存在，写出点P的位置；若不存在，请简要说明理由；
②如图3，点P在CB的延长线上，作∠APQ=45°，PQ的延长线与AC的延长线相交于点Q，是否存在点P，使△APQ是等腰三角形？若存在，写出点P的位置；若不存在，请简要说明理由．

20．已知：|m|=2，a，b互为相反数，且都不为零，c，d互为倒数．则2a+2b+（$\frac{a}{b}$-3cd）-m的值是-6或-2．

17．

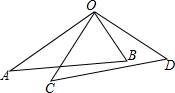如图所示，将一副三角板叠放在一起，使直角顶点重合，且∠AOD=2∠BOC，则∠AOC的等于（　　）

18．如果A、B、C三点在同一直线上，且线段AB=6cm，BC=4cm，若M，N分别为AB，BC的中点，那么M，N两点之间的距离为（　　）

试题分类