题目内容
15. 如图,P为等边△ABC内一点,PA=2,PB=1,PC=$\sqrt{3}$,则△ABC的面积为$\frac{7\sqrt{3}}{4}$.
如图,P为等边△ABC内一点,PA=2,PB=1,PC=$\sqrt{3}$,则△ABC的面积为$\frac{7\sqrt{3}}{4}$.
分析 根据等边三角形的性质BA=BC,∠ABC=60°,则把△BPC绕点B逆时针旋转60°得到△BDA,利用旋转的性质有BD=BP=1,AD=CP=$\sqrt{3}$,∠DBP=∠ABC=60°,△BAD≌△BCP,于是可判断△BDP为等边三角形,所以PD=PB=1,∠BPD=∠BDP=60°,S△BPD=$\frac{\sqrt{3}}{4}$,接着利用勾股定理的逆定理证明∠ADP=90°,则∠APD=60°,S△ADP=$\frac{\sqrt{3}}{2}$,所以S△PAB+S△PBC=S△ADB+S△PAB=S△ADP+S△BPD=$\frac{3\sqrt{3}}{4}$,然后证明△APC为直角三角形,则S△APC=$\sqrt{3}$,所以S△ABC=S△PAB+S△PBC+S△APC=$\frac{7\sqrt{3}}{4}$.
解答  解:∵△ABC为等边三角形,
解:∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
把△BPC绕点B逆时针旋转60°得到△BDA,
∴BD=BP=1,AD=CP=$\sqrt{3}$,∠DBP=∠ABC=60°,△BAD≌△BCP,
∴△BDP为等边三角形,
∴PD=PB=1,∠BPD=∠BDP=60°,S△BPD=$\frac{\sqrt{3}}{4}$×12=$\frac{\sqrt{3}}{4}$,
在△ADP中,∵AD=$\sqrt{3}$,PD=1,PA=2,
∴AD2+PD2=PA2,
∴△ADP为直角三角形,∠ADP=90°,
而PA=2PD,
∴∠APD=60°,S△ADP=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
∴S△PAB+S△PBC=S△ADB+S△PAB=S△ADP+S△BPD=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{4}$=$\frac{3\sqrt{3}}{4}$,
∵∠ADB=∠ADP+∠BDP=90°+60°=150°,
∴∠BPC=150°,
∵∠APB=∠APD+∠BPD=60°+60°=120°,
∴∠APC=360°-150°-120°=90°,
∴△APC为直角三角形,
∴S△APC=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
∴S△ABC=S△PAB+S△PBC+S△APC=$\frac{\sqrt{3}}{4}$+$\sqrt{3}$=$\frac{7\sqrt{3}}{4}$.
故答案为$\frac{7\sqrt{3}}{4}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是勾股定理的应用和证明∠APC=90°.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案| A. | sin55°<cos36° | B. | sin55°>cos36° | C. | sin55°=cos36° | D. | sin55°+cos36°=1 |
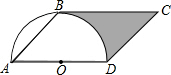 如图,已知?ABCD,∠A=45°,AD=4,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积为6-π(结果保留π).
如图,已知?ABCD,∠A=45°,AD=4,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积为6-π(结果保留π).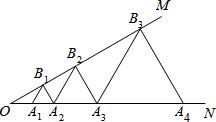 如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为2n.
如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为2n. 一次函数y=-2x+b的图象经过点(1,2).
一次函数y=-2x+b的图象经过点(1,2).