题目内容
12．若方程2x2-3x-m=0两个不相等的实数根，则m的取值范围是m＞-$\frac{9}{8}$．分析 由一元二次方程2x2-3x-m=0有两个不相等的实数根可得△=（-3）2-4×2×（-m）=9+8m＞0，求出m的取值范围即可．
解答 解：∵方程2x2-3x-m=0两个不相等的实数根，
∴△＞0，即△=9-4×2（-m）=9+8m＞0，
∴9+8m＞0，即m＞-$\frac{9}{8}$，
故答案为：m＞-$\frac{9}{8}$．
点评 此题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
阅读快车系列答案
相关题目
如图，正方形ABCD的顶点A，B与正方形EFGH的顶点G，H同在一段抛物线上，且抛物线的顶点同时落在CD和y轴上，正方形边AB与EF同时落在x轴上，若正方形ABCD的边长为4，则正方形EFGH的边长为2$\sqrt{5}$-2．
3．下列式子正确的是（ ）
| A． | sin55°＜cos36° | B． | sin55°＞cos36° | C． | sin55°=cos36° | D． | sin55°+cos36°=1 |
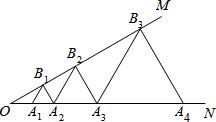如图，已知∠MON=30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA2=4，则△AnBnAn+1的边长为2n．
17．
如图所示，将一副三角板叠放在一起，使直角顶点重合，且∠AOD=2∠BOC，则∠AOC的等于（ ）
如图所示，将一副三角板叠放在一起，使直角顶点重合，且∠AOD=2∠BOC，则∠AOC的等于（ ）| A． | 45° | B． | 30° | C． | 25° | D． | 20° |