题目内容
14. 已知:关于x的一元二次方程mx2-(3m+2)x+2m+2=0(m>0).
已知:关于x的一元二次方程mx2-(3m+2)x+2m+2=0(m>0).(1)求证:方程有两个不相等的实数根;
(2)如果方程的两根都为整数,求整数m的值;
(3)若方程的两个实数根分别为x1,x2(其中x1<x2),y是关于m的函数,且y=x2-2x1,求这个函数的解析式,并结合函数的图象回答:当自变量x的取值范围满足什么条件时,y≤2m.
分析 (1)先计算判别式的值,然后根据判别式的意义即可得到方程总有两个不相等的实数根;
(2)利用求根公式法解方程得到x1=1,x2=$\frac{2m+2}{m}$=1+$\frac{2}{m}$,然后利用有理数的整除性确定m的值;
(3)由(2)可知:x1=1,x2=1+$\frac{2}{m}$,代入y=x2-2x1,求得这个函数的解析式,画出这个函数与y=2m图象,根据交点坐标回答即可.
解答 (1)证明:△=b2-4ac=(3m+2)2-4m(2m+2)=(m+2)2,
∵m>0,(m+2)2>0,即△>0,
∴方程总有两个不相等的实数根.
(2)解:由求根公式得x1=1,x2=$\frac{2m+2}{m}$=1+$\frac{2}{m}$,
∵方程的两个根均为整数且m是整数,
∴1+$\frac{2}{m}$是整数,即$\frac{2}{m}$是整数,
而m>0,
∴m=1或2.
(3)解:x1=1,x2=$\frac{2m+2}{m}$,代入y=x2-2x1=$\frac{2}{m}$在同一平面直角坐标系中分别画出y=$\frac{2}{m}$(m>0)与y=2m(m>0)的图象.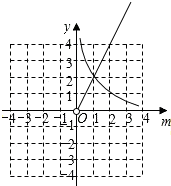
由图象可得,当m≥1时,y≤2m.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.以及解方程的方法.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
4.如图是数值转换机的示意图,小明按照其对应系画出了y与x的函数图象.
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式;
(2)求出所有输出y的值的最小数值;
(3)当输出y的值为3时,求x的值.
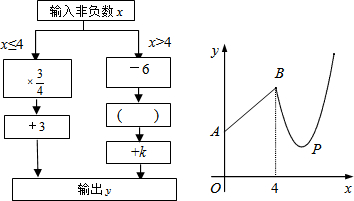
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式;
(2)求出所有输出y的值的最小数值;
(3)当输出y的值为3时,求x的值.

2.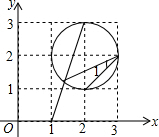 如图,∠1的正切值为( )
如图,∠1的正切值为( )
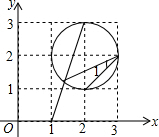 如图,∠1的正切值为( )
如图,∠1的正切值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
9.下列计算错误的是( )
| A. | (23)2×24=210 | B. | (-c)3(-c)5=c8 | C. | 32×(-3)4=(-3)6 | D. | 5×(-$\frac{1}{2}$)2=20 |
19.关于函数y=-$\frac{1}{2}$x,下列结论正确的是( )
| A. | 函数图象必经过点(-1,2) | B. | 函数图象经过第二、四象限 | ||
| C. | y随x的增大而增大 | D. | 不论x取何值,总有y>0 |
 如图,两圆轮叠靠在墙边,已知两轮半径分别为1和4,它们与墙的切点为A,B,则小圆轮上最高点与地面间的距离为9.
如图,两圆轮叠靠在墙边,已知两轮半径分别为1和4,它们与墙的切点为A,B,则小圆轮上最高点与地面间的距离为9.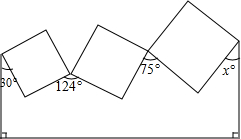 如图,三个正方形一些顶点标出了角的度数,则x=41.
如图,三个正方形一些顶点标出了角的度数,则x=41.