题目内容
5．某商店有两个进价不同的计算器都以64元卖出，其中一个盈利60%，另一个亏本20%，则该商店在这次买卖中（ ）| A． | 不赔不赚 | B． | 赚了8元 | C． | 赔8元 | D． | 赚32元 |
分析 根据题意设一个价钱为x元，另一个价钱为y元，列出方程，求出未知数的值，再计算即可．
解答 解：设一个价钱为x元，另一个价钱为y元，依题意得：
x（1+60%）=64，
y（1-20%）=64，
所以：x=40，y=80，
则64×2-（x+y）=128-120=8．
即：盈利8元．
故选：B．
点评 此题比较简单，考查了一元一次方程的应用．要熟知有理数的运算法则．解答此题的关键是求出计算器的进价．
练习册系列答案
相关题目
1．光明文具厂工人的工作时间：每月26天，每天8小时．待遇：按件计酬，多劳多得，每月另加福利工资920元，按月结算．该厂生产A，B两种型号零件，工人每生产一件A种型号零件，可得报酬0.85元，每生产一件B种型号零件，可得报酬1.5元，下表记录的是工人小王的工作情况：
根据上表提供的信息，请回答如下问题：
（1）小王每生产一件A种型号零件、每生产一件B种型号零件，分别需要多少分钟？
（2）设小王某月生产A种型号零件x件，该月工资为y元，求y与x的函数关系式；
（3）如果生产两种型号零件的数目无限制，那么小王该月的工资数目最多为多少？
| 生产A种型号零件/件 | 生产B种型号零件/件 | 总时间/分 |
| 2 | 2 | 70 |
| 6 | 4 | 170 |
（1）小王每生产一件A种型号零件、每生产一件B种型号零件，分别需要多少分钟？
（2）设小王某月生产A种型号零件x件，该月工资为y元，求y与x的函数关系式；
（3）如果生产两种型号零件的数目无限制，那么小王该月的工资数目最多为多少？
开学初，小明到文具批发部一次性购买某种笔记本，该文具批发部规定：这种笔记本售价y（元/本）与购买数量x（本）之间的函数关系如图所示．
10．
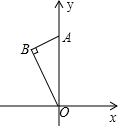如图，含有30°的Rt△AOB的斜边OA在y轴上，且BA=3，∠AOB=30°，将Rt△AOB绕原点O顺时针旋转一定的角度，使直角顶点B落在x轴的正半轴上，得相应的△A′OB′，则A点运动的路程长是（ ）
如图，含有30°的Rt△AOB的斜边OA在y轴上，且BA=3，∠AOB=30°，将Rt△AOB绕原点O顺时针旋转一定的角度，使直角顶点B落在x轴的正半轴上，得相应的△A′OB′，则A点运动的路程长是（ ）| A． | 4π | B． | 5π | C． | 6π | D． | 7π |
15．小聪在用列表尝试法解二元一次方程组时，因风一吹书翻乱忘记了方程组，可清晰地记得一个方程是x+y=6，不妨设另一个方程为ax+by=m，他尝试列表的部分结果如表：
则a-b=150．
| x | … | 3 | 4 | … |
| y | … | 3 | 2 | … |
| ax+by | … | 1350 | 1500 | … |