题目内容
19.如图,在平面直角坐标系中,点O是原点,矩形OABC的顶点A在x轴的正半轴上,顶点C在y的正半轴上,点B的坐标是(4,2),抛物线y=$\frac{1}{2}$x2+bx+c,经过A,C两点,与x轴的另一个交点是点D,连接BD.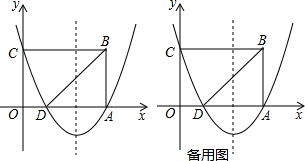
(1)求抛物线的解析式;
(2)点M是抛物线对称轴上的一点,以M,B,D为顶点的三角形的面积是6,求点M的坐标.
(3)若点Q是y轴上一点,且△DBQ为等腰三角形,直接写出点Q的坐标.
分析 (1)求出点A、C的坐标,利用待定系数法求出抛物线的解析式;
(2)如答图1所示,关键是求出MG的长度,利用面积公式解决;注意,符合条件的点M有2个,不要漏解;
(3)分别以BD为底边、BD为腰B为顶点,BD为腰D为顶点三种情况分类讨论确定点Q的坐标即可.
解答 解:(1)∵矩形ABCD,B(4,2),
∴A(4,0),C(0,2).
∵点A(4,0),C(0,2)在抛物线y=$\frac{1}{2}$x2+bx+c上,
∴$\left\{\begin{array}{l}{\frac{1}{2}×16+4b+c=0}\\{c=2}\end{array}\right.$,
解得:b=-$\frac{5}{2}$,c=2.
∴抛物线的解析式为:y=$\frac{1}{2}$x2-$\frac{5}{2}$x+2.
(2)如答图1所示,
∵y=$\frac{1}{2}$x2-$\frac{5}{2}$x+2=$\frac{1}{2}$(x-$\frac{5}{2}$)2-$\frac{9}{8}$,
∴抛物线的对称轴为直线x=$\frac{5}{2}$.
如答图1所示,设对称轴与BD交于点G,与x轴交于点H,则H($\frac{5}{2}$,0).
令y=0,即$\frac{1}{2}$x2-$\frac{5}{2}$x+2,解得x=1或x=4.
∴D(1,0),
∴DH=1.5,AH=1.5,AD=3.
∵tan∠ADB=$\frac{AB}{AD}$=$\frac{2}{3}$,
∴GH=DH•tan∠ADB=$\frac{3}{2}$×$\frac{2}{3}$=1,
∴G($\frac{3}{2}$,1).
∵S△MBD=6,即S△MDG+S△MBG=6,
∴$\frac{1}{2}$MG•DH+$\frac{1}{2}$MG•AH=6,
即:$\frac{1}{2}$MG×$\frac{3}{2}$+$\frac{1}{2}$MG×$\frac{3}{2}$=6,
解得:MG=2.
∴点M的坐标为($\frac{5}{2}$,3)或($\frac{5}{2}$,-1);
(3)当以BD为底边长时,
∵B(4,2),D(1,0),
∴设BD的解析式为y=kx+b,
故$\left\{\begin{array}{l}{4k+b=2}\\{k+b=0}\end{array}\right.$,
解得:k=$\frac{2}{3}$,b=-$\frac{2}{3}$,
∴直线BD的解析式为y=$\frac{2}{3}$x-$\frac{2}{3}$,
∵Q1E垂直平分BD,E($\frac{5}{2}$,1),
∴直线Q1E的解析式为y=-$\frac{3}{2}$x+$\frac{19}{4}$,
∴Q1(0,$\frac{19}{4}$);
当以BD为腰且以B为顶点时,
∵BD=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$<BC,
∴此时不存在点Q;
当以BD为腰且以D为顶点时,
此时OQ=$\sqrt{(\sqrt{13})^{2}-{1}^{2}}$=2$\sqrt{3}$,
∴Q2(0,2$\sqrt{3}$),Q3(0,-2$\sqrt{3}$),
∴存在Q1(0,$\frac{19}{4}$)、Q2(0,2$\sqrt{3}$),Q3(0,-2$\sqrt{3}$)使得△DBQ为等腰三角形.
点评 本题是二次函数综合题型,考查了二次函数的图象与性质、待定系数法、图形面积、解直角三角形、勾股定理等知识点.分类讨论的数学思想是本题考查的重点,在第(2)(3)问中均有所体现,解题时注意全面分析、认真计算.

 阅读快车系列答案
阅读快车系列答案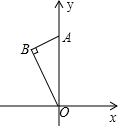 如图,含有30°的Rt△AOB的斜边OA在y轴上,且BA=3,∠AOB=30°,将Rt△AOB绕原点O顺时针旋转一定的角度,使直角顶点B落在x轴的正半轴上,得相应的△A′OB′,则A点运动的路程长是( )
如图,含有30°的Rt△AOB的斜边OA在y轴上,且BA=3,∠AOB=30°,将Rt△AOB绕原点O顺时针旋转一定的角度,使直角顶点B落在x轴的正半轴上,得相应的△A′OB′,则A点运动的路程长是( )| A. | 4π | B. | 5π | C. | 6π | D. | 7π |

| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
 如图,一次函数的y=kx+b图象经过A(2,4)、B(0,2)两点,与x轴交于点C,则△AOC的面积为4.
如图,一次函数的y=kx+b图象经过A(2,4)、B(0,2)两点,与x轴交于点C,则△AOC的面积为4. 已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).
已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).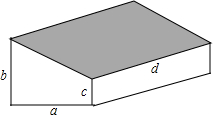 如图,要修建一个蔬菜大棚,棚的横截面是直角梯形,棚宽a=6米,棚高分别为b=5米,c=2米,长为d=30米,现要在棚顶覆盖塑料膜(即图中阴影部分),求共计需要塑料膜多少平方米?
如图,要修建一个蔬菜大棚,棚的横截面是直角梯形,棚宽a=6米,棚高分别为b=5米,c=2米,长为d=30米,现要在棚顶覆盖塑料膜(即图中阴影部分),求共计需要塑料膜多少平方米?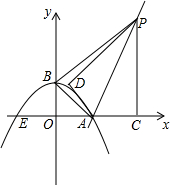 已知:如图,抛物线y=ax2+bx+c与x轴交于点A(4,0)、E(-2,0)两点,与y轴交于点B(0,2,),连结AB.过点A作直线AK⊥AB,动点P从点A出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.
已知:如图,抛物线y=ax2+bx+c与x轴交于点A(4,0)、E(-2,0)两点,与y轴交于点B(0,2,),连结AB.过点A作直线AK⊥AB,动点P从点A出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.