题目内容
6．
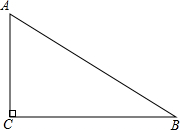除了大家熟知的创建全国文明城市外，淮北目前也正在创建全国绿化模范城市，其中把原有的绿地扩充改造就是创建工程计划之一．如图，现有一块直角三角形的绿地，量得两直角边分别为9米和12米，需要将绿地扩大改造为等腰三角形，且扩充的部分是以BC边为直角边的直角三角形，求扩充后等腰三角形的周长．
分析 根据题目要求扩充成BC为直角边的等腰直角三角形，∠C=90°，然后由勾股定理求得AB的长，最后求出扩充后的等腰直角三角形的周长即可．
解答 解：（1）AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15（m）．
（2）①如图1，延长AC到D，使AC=CD=9m，连接BD，则AB=BD=15时，可求得△ABD的周长为：9+9+15+15=48（m）；
②如图2，延长AC到D，使AD=AB=15m，连接BD，则CD=15-9=6（m），
可求得△ABD的周长为：9+9+15+15=48（m）；
③如图3，当AB为底时，设AD=BD=x，则CD=x-6，由勾股定理得：x=$\frac{25}{3}$，
得△ABD的周长为 $\frac{80}{3}$m．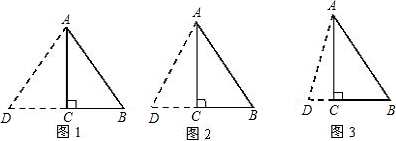 
点评 本题考查的是勾股定理在实际生活中的运用，在解答此题时要注意分三种情况讨论，不要漏解．
练习册系列答案
相关题目
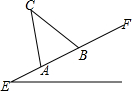如图，为迎接全国文明城市检查，某单位准备在一斜坡EF上安装衣服悬挂“社会主义核心价值观”宣传牌的金属架A-C-B，若CA与地面垂直，斜坡的坡角∠E=30°，∠C=45°，小王测得从A到B的距离是5m，已知每米金属架106元，请你帮该单位算一下安装这副金属架共需多少元（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732，$\sqrt{5}$≈2.236，$\sqrt{6}$≈2.449，结果保留整数）．
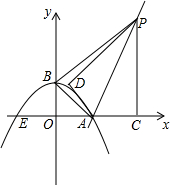已知：如图，抛物线y=ax2+bx+c与x轴交于点A（4，0）、E（-2，0）两点，与y轴交于点B（0，2，），连结AB．过点A作直线AK⊥AB，动点P从点A出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动，设运动时间为t秒，过点P作PC⊥x轴，垂足为C，把△ACP沿AP对折，使点C落在点D处．
18．已知二次函数y=ax2+bx+c（a≠0）与x轴的交点坐标为A（m，0），B（n，0），点A在点B的左边，当ax2+bx+c=2015时有实数根x1，x2（x1＜x2），以下说法中不正确的是（ ）
| A． | 当a＞0时，x1＜m＜n＜x2 | |
| B． | 当a＜0时，m＜x1＜x2＜n | |
| C． | 存在m+n=x1+x2 | |
| D． | y=ax2+bx+c-2015与x轴的交点坐标不可能是（x1，0），（x2，0） |
15．小聪在用列表尝试法解二元一次方程组时，因风一吹书翻乱忘记了方程组，可清晰地记得一个方程是x+y=6，不妨设另一个方程为ax+by=m，他尝试列表的部分结果如表：
则a-b=150．
| x | … | 3 | 4 | … |
| y | … | 3 | 2 | … |
| ax+by | … | 1350 | 1500 | … |