题目内容
9. (1)探究一
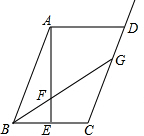
(1)探究一如图,在?ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若$\frac{AF}{BF}$=3,求$\frac{CD}{CG}$的值.
(2)探究二
如图,在?ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若$\frac{AF}{BF}$=m(m>0),则$\frac{CD}{CG}$的值是$\frac{m}{2}$(用含m的代数式表示),试写出解答过程.
(3)探究三
如图,在?ABCD中,点E是BC边上的点,且$\frac{BE}{EC}=n(n>0)$,点F是线段AE上一点,BF的延长线交射线CD于点G,若$\frac{AF}{BF}$=m(m>0),则$\frac{CD}{CG}$的值是$\frac{mn}{n+1}$
(不写解答过程)
分析 (1)本问体现“特殊”的情形,$\frac{AF}{BF}$=3是一个确定的数值.如答图1,过E点作平行线,构造相似三角形,利用相似三角形和中位线的性质,分别将各相关线段均统一用EH来表示,最后求得比值;
(2)本问体现“一般”的情形,$\frac{AF}{BF}$=m不再是一个确定的数值,但(1)问中的解题方法依然适用,如答图2所示;
(3)本问体现“类比”与“转化”的情形,将(1)(2)问中的解题方法推广转化到(3)中,如答图3所示.
解答 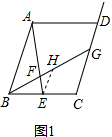 解:(1)依题意,过点E作EH∥AB交BG于点H,如图1所示.
解:(1)依题意,过点E作EH∥AB交BG于点H,如图1所示.
,则有△ABF∽△EHF,
∴$\frac{AB}{EH}$=$\frac{AF}{EF}$=3,
∴AB=3EH.
∵?ABCD,EH∥AB,
∴EH∥CD,
又∵E为BC中点,
∴EH为△BCG的中位线,
∴CG=2EH.
∴$\frac{CD}{CG}$=$\frac{AB}{CG}$=$\frac{3EH}{2EH}$=$\frac{3}{2}$;
(2)如图2,作EH∥AB交BG于点H,则△EFH∽△AFB.
∴$\frac{AB}{EH}$=$\frac{AF}{EF}$=m,
∴AB=mEH.
∵AB=CD,
∴CD=mEH.
∵EH∥AB∥CD,
∴△BEH∽△BCG.
∴$\frac{CG}{EH}$=$\frac{BC}{BE}$=2,
∴CG=2EH.
∴$\frac{CD}{CG}$=$\frac{m}{2}$.
故答案为:$\frac{m}{2}$.
(3)如图3,所示,作EH∥AB交BG于点H,则△EFH∽△AFB.
∴$\frac{AB}{EH}$=$\frac{AF}{EF}$=m,
∴AB=mEH.
∵AB=CD,
∴CD=mEH.
∵EH∥AB∥CD,
∴△BEH∽△BCG,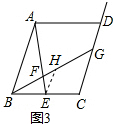
∴$\frac{CG}{EH}$=$\frac{BC}{BE}$,∵$\frac{BE}{EC}=n(n>0)$,
∴$\frac{BC}{BE}=\frac{n+1}{n}$,
∴CG=$\frac{n+1}{n}$EH.
∴$\frac{CD}{CG}$=$\frac{mEH}{\frac{n+1}{n}EH}$=$\frac{mn}{n+1}$,
故答案为:$\frac{mn}{n+1}$.
点评 (1)此题主要考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.
(2)此题还考查了类比、转化、从特殊到一般等思想方法,以及数形结合思想的应用,要熟练掌握.

| A. | 3x+6=0 | B. | $\frac{2}{3}$x=2 | C. | 5-3x=1 | D. | 3(x-1)=x+1 |
| A. | 3.5×10-5 | B. | 3.5×10-4 | C. | 0.35×10-4 | D. | 3.5×10-6 |
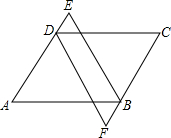 如图,已知AB=CD,AD=BC,DE=BF,说明BE=DF.
如图,已知AB=CD,AD=BC,DE=BF,说明BE=DF.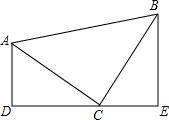 已知,如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥DE于D,BE⊥DE于E,若AD=2cm,BE=3cm,求DE的长.
已知,如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥DE于D,BE⊥DE于E,若AD=2cm,BE=3cm,求DE的长.