题目内容
14．
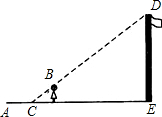如图，小亮欲测量一建筑物的高度．他站在该建筑物的影子上，前后移动，直到他本身影子的顶端正好与建筑物影子的顶端重叠．此时，他距离该建筑物18米．小亮的身高是1.6米，他的影子长是2米，那么该建筑物的高度是16米．
分析 利用相似三角形的判定与性质得出$\frac{CF}{EC}$=$\frac{BF}{DE}$，进而得出答案．
解答 
解：如图所示：可得△CFB∽△CED，
则$\frac{CF}{EC}$=$\frac{BF}{DE}$，
即$\frac{2}{2+18}$=$\frac{1.6}{DE}$
解得：DE=16，
故该建筑物的高度是16m．
故答案为：16米．
点评 此题主要考查了相似三角形的应用，根据题意得出△CFB∽△CED是解题关键．
练习册系列答案
相关题目
4．
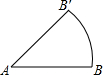如图，将长度为2的线段AB绕点A逆时针旋转45°至AB′，则扇形ABB′的面积为（ ）
如图，将长度为2的线段AB绕点A逆时针旋转45°至AB′，则扇形ABB′的面积为（ ）| A． | $\frac{π}{2}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | π |
9．在Rt△ABC中，∠C=90°，$cosB=\frac{1}{2}$，则∠A的度数为（ ）
| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
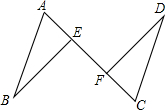如图，线段AB∥CD，AB=CD=$\sqrt{10}$，连接AC，E、F是AC上的两点，且BE∥DF．
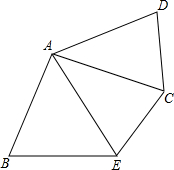如图所示，△ACD是由△ABE旋转得到，∠B=∠D=65°，BA⊥AC，求∠EAC的度数．