题目内容
3. 如图所示,△ACD是由△ABE旋转得到,∠B=∠D=65°,BA⊥AC,求∠EAC的度数.
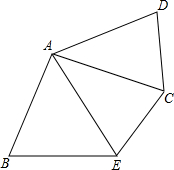
如图所示,△ACD是由△ABE旋转得到,∠B=∠D=65°,BA⊥AC,求∠EAC的度数.
分析 根据垂直定义得∠BAC=90°,再利用旋转的性质得∠AEB=∠D=65°,则利用三角形内角和定理可计算出∠BAE=50°,然后利用互余计算∠EAC的度数.
解答 解:∵BA⊥AC,
∴∠BAC=90°,
∵△ACD是由△ABE旋转得到,
∴∠AEB=∠D=65°,
∵∠B=65°,
∴∠BAE=180°-65°-65°=50°,
∴∠EAC=∠BAC-∠BAE=90°-50°=40°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
13.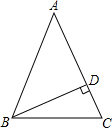 如图,在△ABC中,AB=AC,BD⊥AC,垂足为D,则∠DBC等于( )
如图,在△ABC中,AB=AC,BD⊥AC,垂足为D,则∠DBC等于( )
 如图,在△ABC中,AB=AC,BD⊥AC,垂足为D,则∠DBC等于( )
如图,在△ABC中,AB=AC,BD⊥AC,垂足为D,则∠DBC等于( )| A. | $\frac{1}{2}$∠A | B. | $\frac{1}{2}$∠B | C. | $\frac{1}{2}$(90°-∠B) | D. | $\frac{1}{2}$(90°-∠A) |
11.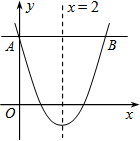 如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
 如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
如图,抛物线y=ax2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )| A. | (2,3) | B. | (3,2) | C. | (3,4) | D. | (4,3) |
10.一个袋中装有标记数分别为-2,1,6的三张卡片(除标记外完全相同),先从袋中随机取出一张卡片,把卡片上标记数作为点A的横坐标,放回后再从袋中随机取出一张卡片,把标记数作为点A的纵坐标,则点A在第一象限的概率是( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
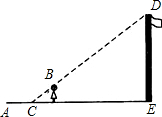 如图,小亮欲测量一建筑物的高度.他站在该建筑物的影子上,前后移动,直到他本身影子的顶端正好与建筑物影子的顶端重叠.此时,他距离该建筑物18米.小亮的身高是1.6米,他的影子长是2米,那么该建筑物的高度是16米.
如图,小亮欲测量一建筑物的高度.他站在该建筑物的影子上,前后移动,直到他本身影子的顶端正好与建筑物影子的顶端重叠.此时,他距离该建筑物18米.小亮的身高是1.6米,他的影子长是2米,那么该建筑物的高度是16米.


