题目内容
15. 如图扇形OAB中,C是$\widehat{AB}$上一动点(不与A,B重合),CD┴OB于D,P为△COD的内心,则∠BPO为( )
如图扇形OAB中,C是$\widehat{AB}$上一动点(不与A,B重合),CD┴OB于D,P为△COD的内心,则∠BPO为( )| A. | 120° | B. | 135° | C. | 150° | D. | 无法确定 |
分析 如图,连接PC.首先证明∠OPC=135°,再由△POC≌△POB,可得∠OPB=∠OPC=135°,解决问题.
解答 解:如图,连接PC.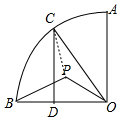
∵P是△CDO的内心,
∴∠PCO=∠PCD,∠POC=∠POD,
∵CD⊥OB,
∴∠CDO=90°,
∴∠PCO+∠POC=45°,
∴∠OPC=135°,
在△POC和△POB中,
$\left\{\begin{array}{l}{OP=OP}\\{∠POC=∠POB}\\{OC=OB}\end{array}\right.$,
∴△POC≌△POB,
∴∠OPB=∠OPC=135°,
故选B.
点评 本题考查三角形的内切圆与内心、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,属于中考常考题型.

练习册系列答案
相关题目
3.方程x2+2x-5=0经过配方后,其结果正确的是( )
| A. | (x+1)2=5 | B. | (x-1)2=5 | C. | (x+1)2=6 | D. | (x-1)2=6 |
 如图,矩形ABCD的对角线AC=10,BC=8,求图中五个小矩形的周长之和.
如图,矩形ABCD的对角线AC=10,BC=8,求图中五个小矩形的周长之和. 如图是由三棱柱、长方体、圆柱三种几何体组成的物体.
如图是由三棱柱、长方体、圆柱三种几何体组成的物体.