题目内容

7．若一个一元二次方程的两个根分别是1、3，请写出一个符合题意的一元二次方程x2-4x+3=0．

分析 先计算出1与3的和、积，然后根据根与系数的关系写出满足条件的一元二次方程．

解答 解：∵1+3=4，1×3=3，
∴以1和3为根的一元二次方程可为x2-4x+3=0．
故答案为x2-4x+3=0．

点评 本题考查了根与系数的关系．一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系为：x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．

练习册系列答案
相关题目
15．如图是一个圆柱体，则从正上方看到的图形是（　　）
A．等腰三角形B．等边三角形C．一个点D．圆
18．如图，已知线段AB=60，点C、D分别是线段AB上的两点，且满足AC：CD：DB=3：4：5，点K是线段CD的中点，求线段KB的长．
解：设AC=3x，则CD=4x，DB=5x，
∵AB=AC+CD+DB=60
∴AB=3x+4x+5x（用含x的代数式表示）=60．
∴x=5．
∵点K是线段CD的中点．
∴KD=$\frac{1}{2}$CD=10．
∴KB=KD+DB=35．
15．如图扇形OAB中，C是$\widehat{AB}$上一动点（不与A，B重合），CD┴OB于D，P为△COD的内心，则∠BPO为（　　）
A．120°B．135°C．150°D．无法确定
2．在图中，你能量出点A到BC边所在直线的距离吗？（先作图，再度量）
表述为：过点A作AD⊥直线BC交BC的延长线于点D．
12．当a=2时，其值为零的分式是（　　）
A．$\frac{a-2}{（a-2）^{2}}$B．$\frac{2a-4}{a-1}$C．$\frac{1}{a-2}$D．$\frac{a+2}{2a}$
19．单项式$\frac{12}{5}$πR2的系数是$-\frac{12}{5}{π^{\;}}$，次数是2．
16．计算：
（1）-12014-$\root{3}{27}$×（-$\frac{1}{2}$）-2+（π-$\sqrt{2}$）0-|-4|+$\sqrt{9}$
（2）（a2b-2ab2-b3）÷b-（a+b）（a-b）．
17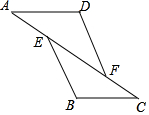．如图，已知AE=CF，∠A=∠C，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（　　）
A．∠D=∠BB．BE=DFC．AD=CBD．BE∥DF

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网