题目内容
10.用适当的方法解下列一元二次方程:(1)(x-1)2+2x(x-1)=0;
(2)3y2+1=2$\sqrt{3}$y;
(3)2(x-3)2=x2-9.
分析 (1)利用因式分解法解方程.
(2)运用公式法求解;
(3)利用因式分解法解方程.
解答 解:(1)(x-1)2+2x(x-1)=0;
(x-1)(x-1+2x)=0
x-1=0,3x-1=0,
∴x1=1,x2=$\frac{1}{3}$;
(2)3y2+1=2$\sqrt{3}$y
∵a=3,b=-2$\sqrt{3}$,c=1,
∴△=b2-4ac=12-12=0,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{2\sqrt{3}}{2×3}$=$\frac{\sqrt{3}}{3}$,
∴x1=x2=$\frac{\sqrt{3}}{3}$;
(3)2(x-3)2=x2-9,
2(x-3)2-(x+3)(x-3)=0
(x-3)(2x-6-x-3)=0,
x-3=0,x-9=0,
∴x1=3,x2=9.
点评 本题考查了解一元二次方程的方法,当把方程通过移项把等式的右边化为0后方程的左边能因式分解时,一般情况下是把左边的式子因式分解,再利用积为0的式子的特点解出方程的根.因式分解法是解一元二次方程的一种简便方法,要会灵活运用.当化简后不能用分解因式的方法即可考虑求根公式法,此法适用于任何一元二次方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.如果$\sqrt{(1-2a)^{2}}$=1-2a,那么( )
| A. | a<$\frac{1}{2}$ | B. | a≤$\frac{1}{2}$ | C. | a>$\frac{1}{2}$ | D. | a≥$\frac{1}{2}$ |
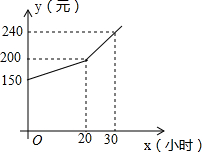 为了鼓励小强做家务,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费用为y元,则y(元)和x(小时)之间的函数图象如图所示.
为了鼓励小强做家务,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费用为y元,则y(元)和x(小时)之间的函数图象如图所示. 如图所示,炮兵在地面C点观察到空中B点有一架敌机,仰角为45°,敌机在同一高度作直线飞行,经过D点到达A点时炮兵观测的仰角为30°,而D点位于炮兵阵地C的正上方2000米处,该敌机从B点飞到A点用1分钟,求敌机的飞行速度.
如图所示,炮兵在地面C点观察到空中B点有一架敌机,仰角为45°,敌机在同一高度作直线飞行,经过D点到达A点时炮兵观测的仰角为30°,而D点位于炮兵阵地C的正上方2000米处,该敌机从B点飞到A点用1分钟,求敌机的飞行速度. 如图,点C,D分别为线段AB(端点A,B除外)上的两个不同的动点,点D始终在点C右侧,图中所有线段的和等于30cm,且AB=3CD,则CD=3cm.
如图,点C,D分别为线段AB(端点A,B除外)上的两个不同的动点,点D始终在点C右侧,图中所有线段的和等于30cm,且AB=3CD,则CD=3cm.