题目内容
6.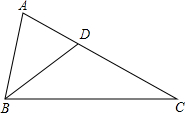 如图,已知BD是∠ABC的角平分线,且∠C=∠DBC,∠BDA=72°,求△ABC各内角度数.
如图,已知BD是∠ABC的角平分线,且∠C=∠DBC,∠BDA=72°,求△ABC各内角度数.
分析 由∠C=∠DBC、∠BDA=72°结合三角形外角的性质,即可得出∠C=∠DBC=36°,由BD是∠ABC的角平分线可求出∠ABC=2∠DBC=72°,再利用三角形内角和定理即可求出∠A的度数.
解答 解:∵∠C=∠DBC,∠BDA=∠C+∠DBC=72°,
∴∠C=∠DBC=36°.
∵BD是∠ABC的角平分线,
∴∠ABC=2∠DBC=72°,
∴∠A=180°-∠ABC-∠C=72°.
点评 本题考查了三角形内角和定理、角平分线以及三角形外角的性质,牢记“三角形内角和是180°”是解题的关键.

练习册系列答案
相关题目
7.生态文明贵阳国际论坛作为我国目前唯一以生态文明为主题的国家级国际性论坛,现已被纳入国家“一带一路”总体规划,持续四届的成功举办,已相继吸引近7000名各国政要及嘉宾出席,7000这个数用科学记数法可表示为( )
| A. | 70×102 | B. | 7×103 | C. | 0.7×104 | D. | 7×104 |
17.已知直线l1:y=-$\frac{2}{3}$x+$\frac{2}{3}$a与直线l2:y=$\frac{3}{2}$x-$\frac{a-1}{2}$的交点在第二象限,则a的取值范围是( )
| A. | -$\frac{1}{2}$<a<$\frac{3}{7}$ | B. | a>-$\frac{1}{2}$ | C. | a$<\frac{3}{7}$ | D. | -$\frac{1}{2}$≤a≤$\frac{3}{7}$ |
16. 如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC≌△DAE的是( )
如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC≌△DAE的是( )
 如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC≌△DAE的是( )
如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC≌△DAE的是( )| A. | AC=AE | B. | BC=DE | C. | ∠B=∠D | D. | ∠C=∠E |
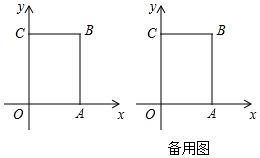 如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a,b满足|a-4|+$\sqrt{b-6}$=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a,b满足|a-4|+$\sqrt{b-6}$=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.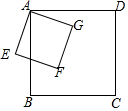 如图,正方形ABCD的边长为2cm,正方形AEFG的边长为1cm,正方形AEFG绕点A旋转的过程中,线段CF的长的最小值为$\sqrt{2}$cm.
如图,正方形ABCD的边长为2cm,正方形AEFG的边长为1cm,正方形AEFG绕点A旋转的过程中,线段CF的长的最小值为$\sqrt{2}$cm.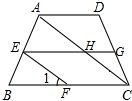 如图,AD∥EG∥BC,AC∥EF,若∠1=50°,则∠AHG=130°.
如图,AD∥EG∥BC,AC∥EF,若∠1=50°,则∠AHG=130°.