题目内容
9.观察下列各式:$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$=1+$\frac{1}{1}$-$\frac{1}{2}$=1$\frac{1}{2}$
$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$=1+$\frac{1}{2}$-$\frac{1}{3}$=1$\frac{1}{6}$
$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$=1+$\frac{1}{3}$-$\frac{1}{4}$=1$\frac{1}{12}$
请你根据上面三个等式提供的信息,猜想:
(1)$\sqrt{1+\frac{1}{{4}^{2}}+\frac{1}{{5}^{2}}}$=1$\frac{1}{20}$
(2)请你按照上面每个等式反映的规律,写出用n(n为正整数)表示的等式:$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n(n+1)}$;
(3)利用上述规律计算:$\sqrt{\frac{50}{49}+\frac{1}{64}}$(仿照上式写出过程)
分析 (1)根据提供的信息,即可解答;
(2)根据规律,写出等式;
(3)根据(2)的规律,即可解答.
解答 解:(1)$\sqrt{1+\frac{1}{{4}^{2}}+\frac{1}{{5}^{2}}}$=1$+\frac{1}{4}-\frac{1}{5}$=1$\frac{1}{20}$;故答案为:1$\frac{1}{20}$;
(2)$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n}-\frac{1}{n+1}$=1+$\frac{1}{n(n+1)}$;故答案为:$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n(n+1)}$;
(3)$\sqrt{\frac{50}{49}+\frac{1}{64}}=\sqrt{1+\frac{1}{{7}^{2}}+\frac{1}{{8}^{2}}}=1\frac{1}{56}$.
点评 本题考查了二次根式的性质与化简,解决本题的关键是关键信息,找到规律.

练习册系列答案
相关题目
10.反比例函数y=$\frac{m-3}{x}$的图象,当x>0时,y随x的增大而增大,则m的取值范围是( )
| A. | m<3 | B. | m≤3 | C. | m>3 | D. | m≥3 |
4.若式子$\sqrt{x-5}$有意义,在实数范围内有意义,则x的取值范围是( )
| A. | x≥5 | B. | x≤5 | C. | x>5 | D. | x<5 |
1.将一张面值100元的人民币兑换成10元或20元的零钱,兑换方案有( )
| A. | 6种 | B. | 5种 | C. | 4 种 | D. | 7种 |
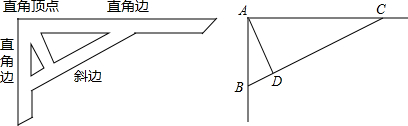
 如图,已知∠ABD=20°,∠ACD=25°,∠A=35°,则∠BDC=80°.
如图,已知∠ABD=20°,∠ACD=25°,∠A=35°,则∠BDC=80°.