题目内容
8．木工师傅为了让直尺经久耐用，常常在直尺的直角顶点与斜边之间加一根小木条（如图①所示），图②为其示意图．若∠BAC=90°，线段AB的长为7，线段AC的长为24，试求出小木条AD的最短长度．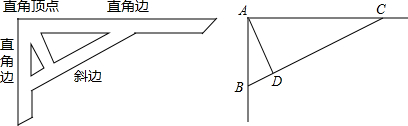
分析 首先利用勾股定理求出BC的长，再利用三角形面积求出即可．
解答 解：∵∠BAC=90°，AB=7，AC=24，
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=25，
当AD⊥BC时，AD最短，则AD×BC=AB×AC，
故25AD=7×24，
解得：AD=$\frac{168}{25}$，
答：小木条AD的最短长度为$\frac{168}{25}$．
点评 此题主要考查了勾股定理的应用以及三角形面积求法，熟练利用三角形面积公式求出是解题关键．
练习册系列答案
相关题目
6．某电动车销售点销售低档、高档两种型号的电动车，每台进价分别为1800元、2700元，下表是近两个月的销售情况：
（注：进价、售价均保持不变，利润=销售收入-进货成本）
（1）求低、高档两种型号的电动车的销售单价；
（2）若该销售点准备用不多于11.7万元的金额再采购这两种型号的电动车共50台，求高档电动车最多能采购多少台；
（3）在（2）的条件下，该销售点销售完这50台电动车能否实现利润为1.4万元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
| 月份 | 销售数量（台） | 销售收入（万元） | |
| 低档 | 高档 | ||
| 3月 | 10 | 10 | 5 |
| 4月 | 15 | 20 | 9 |
（1）求低、高档两种型号的电动车的销售单价；
（2）若该销售点准备用不多于11.7万元的金额再采购这两种型号的电动车共50台，求高档电动车最多能采购多少台；
（3）在（2）的条件下，该销售点销售完这50台电动车能否实现利润为1.4万元的目标？若能，请给出相应的采购方案；若不能，请说明理由．