题目内容
3.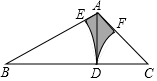 如图,在△ABC中,∠B=30°,∠C=45°,AD是BC边上的高,AB=4cm,分别以B、C为圆心,以BD、CD为半径画弧,交边AB、AC于点E、F,则图中阴影部分的面积是(2$\sqrt{3}$+2-$\frac{3}{2}$π)cm2.
如图,在△ABC中,∠B=30°,∠C=45°,AD是BC边上的高,AB=4cm,分别以B、C为圆心,以BD、CD为半径画弧,交边AB、AC于点E、F,则图中阴影部分的面积是(2$\sqrt{3}$+2-$\frac{3}{2}$π)cm2.
分析 首先计算出AD长,进而可得BD和DC长,然后利用三角形ABC的面积减去扇形BED和DFC的面积即可.
解答 解:∵AD是BC边上的高,
∴∠ADB=∠ADC=90°,
∵∠B=30°,
∴AD=$\frac{1}{2}$AB=2cm,
∴BD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$(cm),
∵∠C=45°,
∴∠DAC=45°,
∴AD=CD=2cm,
∴BC=(2$\sqrt{3}$+2)cm,
∴S阴影=$\frac{1}{2}$×(2$\sqrt{3}$+2)×2-$\frac{30×π×12}{360}$-$\frac{45π×4}{360}$=2$\sqrt{3}$+2-π-$\frac{π}{2}$=2$\sqrt{3}$+2-$\frac{3}{2}$π,
故答案为:(2$\sqrt{3}$+2-$\frac{3}{2}$π).
点评 此题主要考查了扇形的面积计算,以及勾股定理,关键是正确计算出AD、BD、CD长.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 如图,正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是8.
如图,正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是8.
 一次函数y=kx+b的图象如图所示,则不等式kx+b<0的解集为x<1.
一次函数y=kx+b的图象如图所示,则不等式kx+b<0的解集为x<1.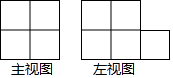 如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最小是5个.
如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最小是5个.