题目内容
15.已知(x-y+3)2+$\sqrt{2x+y}$=0,则x+y=1.分析 利用非负数的性质列出方程组,求出方程组的解得到x与y的值,即可确定出x+y的值.
解答 解:∵(x-y+3)2+$\sqrt{2x+y}$=0,
∴$\left\{\begin{array}{l}{x-y=-3①}\\{2x+y=0②}\end{array}\right.$,
①+②得:3x=-3,即x=-1,
将x=-1代入②得:y=2,
则x+y=2-1=1.
故答案为:1
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
20.我们已经学习过一次函数和反比例函数的图象和性质,类似地可以对函数y=x-$\frac{1}{x}$进行探索.下列结论:①图象在第一、三象限;②图象与y轴无交点;③图象与x轴只有一个交点;④图象关于原点成中心对称;⑤当x>0时,y随x的增大而增大;其中正确的结论是( )
| A. | ①②③ | B. | ①③⑤ | C. | ②④⑤ | D. | ③④⑤ |
7. 一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )
一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )
 一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )
一名射箭运动员统计了45次射箭的成绩,并绘制了如图所示的折线统计图.则在射箭成绩的这组数据中,众数和中位数分别是( )| A. | 18,18 | B. | 8,8 | C. | 8,9 | D. | 18,8 |
5.在函数y=$\frac{\sqrt{x+1}}{x-2}$中,自变量x的取值范围是( )
| A. | x>-1 | B. | x≥-1 | C. | x≥-1且x≠2 | D. | x>-1且x≠2 |
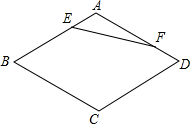 如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF长度的范围是$\frac{\sqrt{3}}{2}$a≤EF≤a.
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF长度的范围是$\frac{\sqrt{3}}{2}$a≤EF≤a.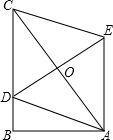 如图,在△ABC中,∠B=90°,AB=5,BC>AB,点D是BC上的动点,四边形ADCE是平行四边形,DE的最小值是5.
如图,在△ABC中,∠B=90°,AB=5,BC>AB,点D是BC上的动点,四边形ADCE是平行四边形,DE的最小值是5.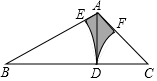 如图,在△ABC中,∠B=30°,∠C=45°,AD是BC边上的高,AB=4cm,分别以B、C为圆心,以BD、CD为半径画弧,交边AB、AC于点E、F,则图中阴影部分的面积是(2$\sqrt{3}$+2-$\frac{3}{2}$π)cm2.
如图,在△ABC中,∠B=30°,∠C=45°,AD是BC边上的高,AB=4cm,分别以B、C为圆心,以BD、CD为半径画弧,交边AB、AC于点E、F,则图中阴影部分的面积是(2$\sqrt{3}$+2-$\frac{3}{2}$π)cm2.