题目内容
1.若关于x的不等式组$\left\{\begin{array}{l}{x-m≤0}\\{7-x<2m}\end{array}\right.$的整数解为1,2,3,则m的取值范围是1≤m<2.分析 先求出每个不等式的解集,根据已知不等式组的整数解得出关于m的不等式组,求出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{x-m≤0①}\\{7-x<2m②}\end{array}\right.$
∵解不等式①得:x≤m,
解不等式②得:x>7-2m,
又∵关于x的不等式组$\left\{\begin{array}{l}{x-m≤0}\\{7-x<2m}\end{array}\right.$的整数解为1,2,3,
∴3<7-2m≤4且1≤m<2,
解得:1≤m<2.
故答案为:1≤m<2.
点评 本题考查了解一元一次不等式,解一元一次不等式组,不等式组的整数解的应用,能根据不等式的解集和已知得出3<7-2m≤4和1≤m<2是解此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
12.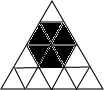 如图是某幼儿园活动室的一个正三角形活动区,老师让小朋友们向这个活动区扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形都是等可能的,扔1次沙包恰好击中阴影区域的概率等于( )
如图是某幼儿园活动室的一个正三角形活动区,老师让小朋友们向这个活动区扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形都是等可能的,扔1次沙包恰好击中阴影区域的概率等于( )
 如图是某幼儿园活动室的一个正三角形活动区,老师让小朋友们向这个活动区扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形都是等可能的,扔1次沙包恰好击中阴影区域的概率等于( )
如图是某幼儿园活动室的一个正三角形活动区,老师让小朋友们向这个活动区扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形都是等可能的,扔1次沙包恰好击中阴影区域的概率等于( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
16.若分式$\frac{x-1}{(x-2)(x-3)}$=$\frac{a}{x-3}$+$\frac{b}{x-2}$(a、b为常数),则a、b的值为( )
| A. | a=4,b=-3 | B. | a=2,b=-1 | C. | a=-1,b=1 | D. | a=-1,b=2 |
13.代数式4x2+1加上下列单项式后,仍不能成为完全平方式的是( )
| A. | 4x4 | B. | 4x | C. | -4x | D. | 2x |
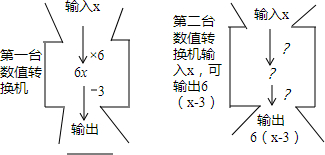
11.第一台转换机的输出结果是:6x-3; 第二台转换机的运算过程为:先-3,再×6
填写下表:
填写下表:

| 输入 | -2 | -$\frac{1}{2}$ | 0 | 0.26 | $\frac{1}{3}$ | $\frac{5}{2}$ | 4.5 |
| 左图的输出 | |||||||
| 右图的输出 |
 已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.
已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.