题目内容
3. 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=15cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以2cm/s的速度向B点运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD,需经过多少时间?为什么?
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=15cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以2cm/s的速度向B点运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD,需经过多少时间?为什么?
分析 设点P、Q运动时间为t秒,得出AP=tcm,CQ=2tcm,PD=12-t,当PQ∥CD且PQ=CD时,得出方程12-t=2t,求出即可;当PQ与CD不平行,PQ=CD时,四边形PQCD为等腰梯形,分别过点P、D作PM⊥BC,DN⊥BC,垂足分别为M、N,则MN=PD=12-t,得出方程$\frac{1}{2}$(3t-12)=3,求出即可.
解答  解:设点P、Q运动时间为t秒,
解:设点P、Q运动时间为t秒,
则AP=tcm,CQ=3tcm,
∵AD=12cm,BC=15cm,
∴PD=AD-AP=12-t,
如图1当PQ∥CD,且PQ=CD时,
∵AD∥BC,即PD∥QC,
∴四边形PQCD为平行四边形,
∴PQ=CD,PD=CQ,
∴12-t=2t,
解得t=4s,即当t=4s时,PQ=CD;
当PQ与CD不平行,PQ=CD时,四边形PQCD为等腰梯形.
如图2,分别过点P、D作PM⊥BC,DN⊥BC,
垂足分别为M、N,则MN=PD=12-t,
QM=CN=$\frac{1}{2}$(CQ-MN)=$\frac{1}{2}$(2t-12+t),
=$\frac{1}{2}$(3t-12),
∵在四边形ABCD中,AD∥BC,∠B=90°,
∴∠A=90°,
∵DN⊥BC,
∴∠BND=90°,
∴四边形ABND为矩形,
∴BN=AD=12,
∴QM=CN=BC-BN=15-12=3,
∴$\frac{1}{2}$(3t-12)=3,解得t=6.
综上,当t=4s或t=6时PQ=CD.
点评 本题考查了梯形的性质,矩形的性质和判定,平行四边形的性质的应用,题目是一道综合性比较强的题目,难度适中.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
18.已知函数自变量的取值范围是$\frac{1}{3}$<x≤1,那么这个函数的解析式可能是( )
| A. | y=$\frac{1-x}{\sqrt{3x-1}}$ | B. | y=$\sqrt{\frac{1-x}{3x-1}}$ | C. | y=$\frac{\sqrt{3x-1}}{1-x}$ | D. | y=$\frac{1}{\sqrt{1-x}}$-$\sqrt{3x-1}$ |
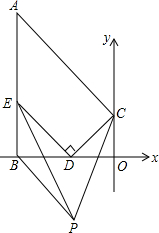 如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.
如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P. 已知:平行四边形ABCD中,AB=2BC,延长CB到E,BE=BC,延长BC到F,CF=BC,AF、DE相交于G,求证:AF⊥DE.
已知:平行四边形ABCD中,AB=2BC,延长CB到E,BE=BC,延长BC到F,CF=BC,AF、DE相交于G,求证:AF⊥DE.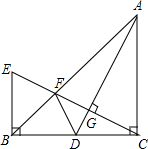 如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.求证:∠ADC=∠BDF.
如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.求证:∠ADC=∠BDF.