题目内容
13.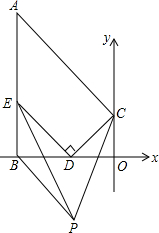 如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.
如图,直线x⊥直线y于点O,直线x⊥AB于点B,E是线段AB上一定点,D点为线段OB上的一动点(点D不与点O、B重合),CD⊥DE交直线y于点C,连接AC,∠BED、∠DCO的角平分线的交点为P.(1)当∠OCD=60°,求∠BED的度数;
(2)当∠CDO=∠A时,有结论:①CD⊥AC,②EP∥AC,其中只有一个结论是正确的,请选择正确的结论,并说明理由;
(3)当点D在线段OB上运动时,问∠P的大小是否为定值?若是定值,求其值,并说明理由;若变化,求其变化范围.
分析 (1)由垂直的定义和三角形的内角和得到结论;
(2)根据平行线的性质得到结论;
(3)利用外角的性质和角平分线的性质求得∠P的大小等于45°是个定值.
解答 解:(1)∵直线x⊥直线y于点O,
∴∠COD=90°,∵∠OCD=60°,
∴∠CDO=30°,
∵∠CDE=90°,
∴∠EDB=60°,
∴∠BED=30°;
(2)①CD⊥AC正确,
由(1)证得;∠CDO=∠BED,
∵∠CDO=∠A,
∴∠BED=∠A,
∴AC∥DE,
∵ED⊥CD,
∴AC⊥CD,
(3)如图连接PD并延长PD,∵∠5=∠3-∠1,∠6=∠4-∠2,
∴∠5+∠6=∠3+∠4-(∠1+∠2),
∵∠3+∠4=90°,∠1+∠2=$\frac{1}{2}$$∠BED+\frac{1}{2}∠DCO$
=$\frac{1}{2}$(∠BED+∠DCO)=$\frac{1}{2}$×90°=45°
∴∠5+∠6=45°,
∴∠EPC=45°是个定值.
点评 本题考查了,平行线的判定和性质,垂线的定义,三角形的内角和,辅助线的作法是关键.

练习册系列答案
相关题目
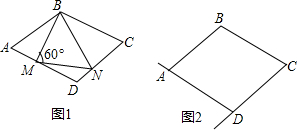
 如图,∠APC=30°,$\widehat{BD}$=30°,则$\widehat{AC}$=90°,∠AEB=120°.
如图,∠APC=30°,$\widehat{BD}$=30°,则$\widehat{AC}$=90°,∠AEB=120°. 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=15cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以2cm/s的速度向B点运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD,需经过多少时间?为什么?
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=15cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以2cm/s的速度向B点运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD,需经过多少时间?为什么?