题目内容
(1)解不等式:1+
>5-
;
(2)计算:
÷(1+
);
(3)解方程:
=
.
| x |
| 3 |
| x-2 |
| 2 |
(2)计算:
| a2-b2 |
| a2b-ab2 |
| a2+b2 |
| 2ab |
(3)解方程:
| 1 |
| x-2 |
| 1-x |
| 2-x |
考点:分式的混合运算,解分式方程,解一元一次不等式
专题:计算题
分析:(1)不等式去分母,去括号,移项合并,将x系数化为1,即可求出解;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分即可得到结果;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分即可得到结果;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答:解:(1)不等式去分母得:6+2x>30-3x+6,
移项合并得:5x>30,
解得:x>6;
(2)原式=
÷
=
•
=
;
(3)去分母得:1=x-1,
解得:x=2,
经检验x=2是增根,分式方程无解.
移项合并得:5x>30,
解得:x>6;
(2)原式=
| (a+b)(a-b) |
| ab(a-b) |
| a2+2ab+b2 |
| 2ab |
| a+b |
| ab |
| 2ab |
| (a+b)2 |
| 2 |
| a+b |
(3)去分母得:1=x-1,
解得:x=2,
经检验x=2是增根,分式方程无解.
点评:此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
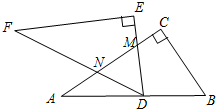 如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN,则重叠部分(△DMN)的面积为
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN,则重叠部分(△DMN)的面积为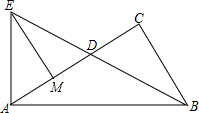 如图,在Rt△ABC中,∠C=90°,点D为AC边上一点,将线段AD绕点A逆时针旋转到线段AE,使得AE⊥AB,且点E、D、B恰好在同一直线上,作EM⊥AC于点M.
如图,在Rt△ABC中,∠C=90°,点D为AC边上一点,将线段AD绕点A逆时针旋转到线段AE,使得AE⊥AB,且点E、D、B恰好在同一直线上,作EM⊥AC于点M. 如图,在△ABC中,AD,BE,CF是三条高,交点为H,延长AH交外接圆于点M,
如图,在△ABC中,AD,BE,CF是三条高,交点为H,延长AH交外接圆于点M,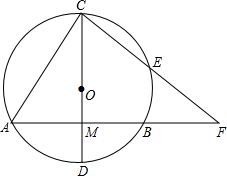 如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交CE的延长线于点F.求:
如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交CE的延长线于点F.求: 如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上,且A(1,-4),B(5,-4),C(4,-1).
如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上,且A(1,-4),B(5,-4),C(4,-1).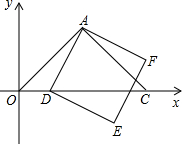 如图,在平面直角坐标中,点A的坐标为(1,1),OA=AC,∠OAC=90°,点D为x轴上一动点.以AD为边在AD的右侧作正方形ADEF.
如图,在平面直角坐标中,点A的坐标为(1,1),OA=AC,∠OAC=90°,点D为x轴上一动点.以AD为边在AD的右侧作正方形ADEF.