题目内容
14. 如图,?ABCD的对角线AC、BD相交于点O,BD=12cm,AC=6cm,点E在线段BO上从点B以1cm/s的速度向点O运动,点F在线段OD上从点O以2cm/s的速度向点D运动.
如图,?ABCD的对角线AC、BD相交于点O,BD=12cm,AC=6cm,点E在线段BO上从点B以1cm/s的速度向点O运动,点F在线段OD上从点O以2cm/s的速度向点D运动.(1)若点E、F同时运动,设运动时间为t秒,当t为何值时,四边形AECF是平行四边形.
(2)在(1)的条件下,当AB为何值时,?AECF是菱形;
(3)求(2)中菱形AECF的面积.
分析 (1)若是平行四边形,所以BD=12cm,则B0=DO=6cm,故有6-1t=2t,即可求得t值;
(2)若是菱形,则AC垂直于BD,即有AO2+BO2=AB2,故AB可求;
(3)根据四边形AECF是菱形,求得BO⊥AC,OE=OF,根据平行四边形的性质得到BO=OD,求得BE=DF,列方程到底BE=DF=2,求得EF=8,于是得到结论.
解答 解:(1)若四边形AECF为平行四边形,
∴AO=OC,EO=OF,
∵四边形ABCD为平行四边形,
∴BO=OD=6cm,
∴EO=6-t,OF=2t,
∴6-t=2t,
∴t=2s,
∴当t为2秒时,四边形AECF是平行四边形;
(2)若四边形AECF是菱形,
∴AC⊥BD,
∴AO2+BO2=AB2,
∴AB=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$;
∴当AB为3$\sqrt{5}$时,?AECF是菱形;
(3)解:(1)若四边形AECF为平行四边形,
∴AO=OC,EO=OF,
∵四边形ABCD为平行四边形,
∴BO=OD=6cm,
∴EO=6-t,OF=2t,
∴6-t=2t,
∴t=2s,
∴当t为2秒时,四边形AECF是平行四边形;
(2)若四边形AECF是菱形,
∴AC⊥BD,
∴AO2+BO2=AB2,
∴AB=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$;
∴当AB为3$\sqrt{5}$时,?AECF是菱形;
(3)∵四边形AECF是菱形,
∴BO⊥AC,OE=OF,
∵四边形ABCD是平行四边形,
∴BO=OD,
∴BE=DF,
∴t=6-2t,
∴t=2,
∴BE=DF=2,
∴EF=8,
∴菱形AECF的面积=$\frac{1}{2}$AC•EF=$\frac{1}{2}×$6×8=24.
点评 本题考查了平行四边形的判定和性质和菱形的判定和性质,勾股定理,菱形的面积的计算,考查学生综合运用数学知识的能力.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
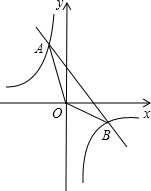 如图所示,一次函数y=kx+b的图象与反比例函数y=-$\frac{8}{x}$的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2,
如图所示,一次函数y=kx+b的图象与反比例函数y=-$\frac{8}{x}$的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2,