题目内容
16.投掷一枚普通的正方体骰子24次.(1)你认为下列四种说法中正确的为④(填序号);
①出现1点的概率等于出现3点的概率;
②投掷24次,2点一定会出现4次;
③投掷前默念几次“出现4点”,投掷结果出现4点的可能性就会加大;
④连续投掷6次,出现的点数之和不可能等于37.
(2)小轩和小宇两个同学玩“掷骰子”游戏,规定:骰子出现点数大的获胜,如果小轩“掷骰子”出现点数为4,那么小宇获胜的概率是多少?
分析 (1)根据随机事件的定义逐一判断即可得;
(2)根据概率公式求解可得.
解答 解:(1)①出现1点的概率可能等于出现3点的概率,此结论错误;
②投掷24次,2点可能会出现4次,此结论错误;
③投掷前默念几次“出现4点”,投掷结果出现4点的可能性不会受其影响,此结论错误;
④连续投掷6次,出现的点数之和最大为36,不可能等于37,此结论正确;
故答案为:④;
(2)小轩“掷骰子”出现点数为4,那么小宇“掷骰子”出现点数可能为1、2、3、4、5、6,
其中小宇抛掷的点数较大的有5、6这2种结果,
∴小宇获胜的概率是$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题主要考查概率公式及随机事件,熟练掌握随机事件的概率计算是解题的关键.

练习册系列答案
相关题目
1.在?ABCD中,下列关于向量的等式正确的是( )
| A. | $\stackrel{→}{AB}$+$\stackrel{→}{CD}$=$\stackrel{→}{0}$ | B. | $\stackrel{→}{AB}$-$\stackrel{→}{AD}$=$\stackrel{→}{BD}$ | C. | $\stackrel{→}{AB}$+$\stackrel{→}{AD}$=$\stackrel{→}{BD}$ | D. | $\stackrel{→}{AB}$+$\stackrel{→}{BD}$=$\stackrel{→}{DA}$ |
8. 如图,下列条件中,能够判定AB∥CD的是( )
如图,下列条件中,能够判定AB∥CD的是( )
 如图,下列条件中,能够判定AB∥CD的是( )
如图,下列条件中,能够判定AB∥CD的是( )| A. | ∠2=∠4 | B. | ∠1=∠2+∠3 | C. | ∠3=∠5 | D. | ∠D+∠4+∠5=180° |
5.一种登革热病毒的直径约为0.00000005m,数据0.00000005m可用科学记数法表示为( )
| A. | 5×10-7m | B. | 5×10-8m | C. | 0.5×10-7m | D. | -5×108m |
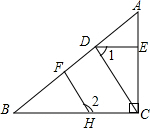 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补.求证:HF⊥AB.
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补.求证:HF⊥AB.
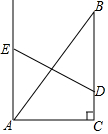 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=4,点D在BC上,以AB为对角线的所有平行四边形ADBE中,DE的最小值是3.
如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=4,点D在BC上,以AB为对角线的所有平行四边形ADBE中,DE的最小值是3. 如图,在△ABC中,∠ACB=90°,M、N、E是△ABC边上的点,且∠1+∠2=90°,试说明MN∥CE.
如图,在△ABC中,∠ACB=90°,M、N、E是△ABC边上的点,且∠1+∠2=90°,试说明MN∥CE.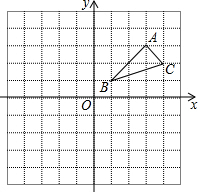 如图在平面直角坐标系中,每个小方格是边长为1的正方形,已知△ABC.
如图在平面直角坐标系中,每个小方格是边长为1的正方形,已知△ABC.