题目内容
1．在?ABCD中，下列关于向量的等式正确的是（ ）| A． | $\stackrel{→}{AB}$+$\stackrel{→}{CD}$=$\stackrel{→}{0}$ | B． | $\stackrel{→}{AB}$-$\stackrel{→}{AD}$=$\stackrel{→}{BD}$ | C． | $\stackrel{→}{AB}$+$\stackrel{→}{AD}$=$\stackrel{→}{BD}$ | D． | $\stackrel{→}{AB}$+$\stackrel{→}{BD}$=$\stackrel{→}{DA}$ |
分析 根据平面向量的平行四边形法则和三角形法则对各选项分析判断即可得解．
解答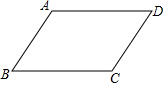 
解：A、$\overrightarrow{AB}$与$\overrightarrow{CD}$的模相等，但是方向相反，则$\stackrel{→}{AB}$+$\stackrel{→}{CD}$=$\stackrel{→}{0}$，故本选项正确；
B、$\overrightarrow{AD}$-$\stackrel{→}{AB}$=$\stackrel{→}{BD}$，故本选项错误；
C、$\overrightarrow{AD}$-$\stackrel{→}{AB}$=$\stackrel{→}{BD}$，故本选项错误；
D、$\overrightarrow{AB}$+$\overrightarrow{DA}$=$\overrightarrow{BD}$，故本选项错误；
故选：A．
点评 本题考查了平面向量，此类题目主要利用了平行四边形法则和三角形法则，要注意$\overrightarrow{0}$与0的不同．
练习册系列答案
相关题目
如图，在一次夏令营活动中，某同学从营地A点出发，先沿北偏东70°方向到达B地，再沿北偏西15°方向去目的地C，则∠ABC的度数是95°．
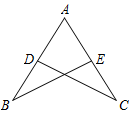如图，点D、E分别在线段AB、AC上，联结BE，CD，BE=CD，要使△ABE≌△ACD，还需添加一个条件，这个条件可以是∠B=∠C（答案不唯一） （只要写一个条件）．
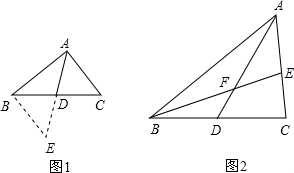某校数学课外兴趣小组活动时，老师提出如下问题：