题目内容
11.一次,陈老师在黑板上写出三个算式:52-32=8×2,92-72=8×4,152-32=8×27,接着陈老师请王华接着写两个具有同样规律的算式,于是王华同学在黑板上写出了如下两个算式:112-52=8×12,152-72=8×32…(1)请你判断王华两个算式是否正确,不必说明理由;并请你再写出两个(不同于上面算式)具有上述规律的算式;
(2)用文字写出反映上述算式的规律;
(3)证明这个规律的正确性.
分析 通过观察可知,等式左边一直是两个奇数的平方差,右边总是8乘以一个数.根据平方差公式,把等式左边进行计算,即可得出结论任意两个奇数的平方差等于8的倍数.
解答 解:(1)112-92=8×5,132-112=8×6.
(2)规律:任意两个奇数的平方差等于8的倍数.
(3)证明:设m,n为整数,两个奇数可表示2m+1和2n+1,
则(2m+1)2-(2n+1)2=4(m-n)(m+n+1).
当m,n同是奇数或偶数时,(m-n)一定为偶数,所以4(m-n)一定是8的倍数.
当m,n一奇一偶时,则(m+n+1)一定为偶数,所以4(m+n+1)一定是8的倍数
所以,任意两奇数的平方差是8的倍数.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,∠AOB是平角,OD、OE分别是∠AOC、∠BOC平分线,∠DOE等于( )
如图,∠AOB是平角,OD、OE分别是∠AOC、∠BOC平分线,∠DOE等于( )
 如图,∠AOB是平角,OD、OE分别是∠AOC、∠BOC平分线,∠DOE等于( )
如图,∠AOB是平角,OD、OE分别是∠AOC、∠BOC平分线,∠DOE等于( )| A. | 105° | B. | 100° | C. | 90° | D. | 80° |
19.下列说法错误的是( )
| A. | 整数与分数统称为有理数 | B. | 最小的正整数是0 | ||
| C. | 负整数,0与正整数统称为整数 | D. | 互为相反数的两个数的和等于0 |
6.已知m-2n=-1,则代数式1-2m+4n的值是( )
| A. | -3 | B. | -1 | C. | 2 | D. | 3 |
3.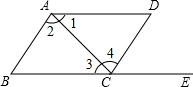 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠1=∠3 | B. | ∠D=∠DCE | C. | ∠2=∠4 | D. | ∠D+∠BCD=180° |
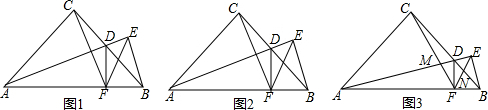
 如图是一束平行光线从教室窗户射入的平面示意图,BC=1,NC=$\frac{4}{3}$,BN=$\frac{5}{3}$,AB=3.5,MN=$\frac{14}{3}$,求AM的长度.
如图是一束平行光线从教室窗户射入的平面示意图,BC=1,NC=$\frac{4}{3}$,BN=$\frac{5}{3}$,AB=3.5,MN=$\frac{14}{3}$,求AM的长度.