题目内容
16.在Rt△ABC中,∠C=90°,∠A=30°,设Rt△ABC的面积为y,BC=x,则y与x之间的函数关系式为$y=\frac{\sqrt{3}}{2}{x}^{2}$.分析 先根据三角函数求出AC的长,然后再利用三角形的面积公式计算即可.
解答 解:∵∠C=90°,∠A=30°,BC=x
∴tan∠A=$\frac{BC}{AC}$,
∴AC=$\frac{BC}{tan∠A}$=$\sqrt{3}x$
∴S△ABC=$\frac{1}{2}BC•AC$
所以y与x的函数关系式为y=$\frac{\sqrt{3}}{2}{x}^{2}$,
故答案是y=$\frac{\sqrt{3}}{2}{x}^{2}$.
点评 此题主要考查了直角三角形的面积公式,求出AC的长是解题的关键.

练习册系列答案
相关题目
6.已知m-2n=-1,则代数式1-2m+4n的值是( )
| A. | -3 | B. | -1 | C. | 2 | D. | 3 |
6.下列叙述中,正确的是( )
| A. | 以点O为圆心,以任意长为半径画弧,交线段OA于点B | |
| B. | 以∠AOB的边OB为一边作∠BOC | |
| C. | 以点O为圆心画弧,交射线OA于点B | |
| D. | 在线段AB的延长线上截取线段BC=AB |
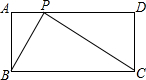 如图,在长方形ABCD中,AB=2$\sqrt{5}$cm,BC=4$\sqrt{5}$cm.点P以$\sqrt{5}$cm/s的速度在长方形边上从点A出发,沿A-D-C的路径运动,到点C停止.
如图,在长方形ABCD中,AB=2$\sqrt{5}$cm,BC=4$\sqrt{5}$cm.点P以$\sqrt{5}$cm/s的速度在长方形边上从点A出发,沿A-D-C的路径运动,到点C停止.