题目内容
14.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A($\frac{3}{2}$,0),B(0,2),则点B2017的坐标为(6052,0).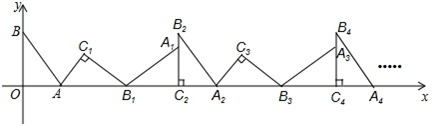
分析 首先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…,即可得每偶数之间的B相差6个单位长度,根据这个规律可以求得B2017的坐标.
解答 解:解:∵AO=$\frac{3}{2}$,BO=2,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\frac{5}{2}$,
∴OA+AB1+B1C2=6,
∴B2的横坐标为:6,且B2C2=2,
∴B4的横坐标为:2×6=12,
∴点B2016的横坐标为:2016÷2×6=6048.
∴点B2016的纵坐标为:2.
∴点B2016的坐标为:(6048,2),
∴B2017的横坐标为6048+$\frac{3}{2}$+$\frac{5}{2}$=6052,
∴点B2017的坐标为(6052,0),
故答案为(6052,0)
点评 此题考查了点的坐标规律变换,通过图形旋转,找到所有B点之间的关系是本题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
6.某市质量监督局从某食品厂生产的罐头中,随意抽取20听进行检查,超过标准质量的用正数表示,不足标准质量的用负数表示,抽查的结果如表:
请问这批样品的平均质量比标准质量多或少多少克?
| 与标准质量的偏差(克) | -10 | -5 | 0 | +5 | +10 | +15 |
| 听数 | 2 | 5 | 4 | 6 | 2 | 1 |
3.为了倡导节约用水,某城市自来水实行阶梯水价收费,收费标准如表:
(1)若月用水量为x吨,试分别写出当x≤10、10<x≤18、x>18时水费的代数式(用含x的式子表示);
(2)若某户居民3月份的水费为25元,该用户这个月用水量为多少吨?
| 月用水量 | 不超过10吨 | 超过10吨但不超过18吨的部分 | 超过18吨的部分 |
| 收费标准(元/吨) | 2.00 | 2.50 | 3.00 |
(2)若某户居民3月份的水费为25元,该用户这个月用水量为多少吨?
 那么第105个图案是①(只填图案序号:①
那么第105个图案是①(只填图案序号:① ,②
,② ,③
,③ ,④
,④ ),前2009个有503个“
),前2009个有503个“ ”.
”.
 如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$与一次函数y2=k2x+b的图象交于点A(1,8)、B(-4,m).
如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$与一次函数y2=k2x+b的图象交于点A(1,8)、B(-4,m).