题目内容
2.阅读材料,解答问题例:用图象法解一元二次不等式:x2-2x-3>0.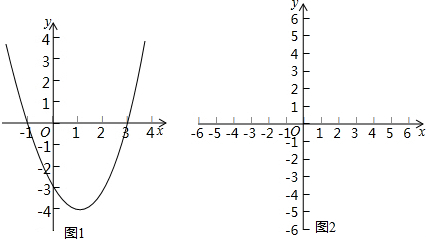
解:设y=x2-2x-3,则y是x的二次函数.
∵a=1>0∴抛物线开口向上.
又∵当y=0时,x2-2x-3=0,解得x1=-1,x2=3.
∴由此得抛物线y=x2-2x-3的大致图象如图所示.
观察函数图象可知:当x<-1或x>3时,y>0.
∴x2-2x-3>0的解集是:x<-1或x>3.
(1)观察图象1,直接写出一元二次不等式:x2-2x-3<0的解集是-1<x<3;
(2)仿照上例,用图象法解一元二次不等式:-x2+4x-3<0.
分析 (1)根据函数图形回答即可;
(2)先判断出抛物线的开口方向,然后求得抛物线与x轴交点坐标,最后根据函数图象进行判断即可.
解答 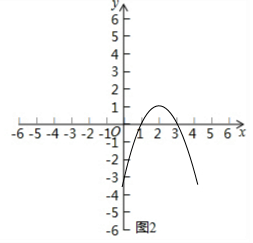 解:(1)观察函数图象可知:当-1<x<3时,y<0.
解:(1)观察函数图象可知:当-1<x<3时,y<0.
∴x2-2x-3<0的解集是:-1<x<3,
故答案为:-1<x<3;
(2)设y=-x2+4x-3,则y是x的二次函数.
∵a=-1<0∴抛物线开口向下,
又∵当y=0时,-x2+4x-3=0,解得x1=1,x2=3,
∴由此得抛物线y═-x2+4x-3的大致图象如图2所示,
观察函数图象可知:当x<1或x>3时,y<0,
∴-x2+4x-3<0的解集是:x<1或x>3.
点评 本题主要考查的是二次函数与不等式组,利用函数图象确定出不等式组的解集是解题的关键.

练习册系列答案
相关题目
15. 已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
 已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )| A. | a<b | B. | a+b>0 | C. | ab<0 | D. | b-a>0 |
10.等腰三角形的周长为2+$\sqrt{3}$,腰长为1,则底角等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: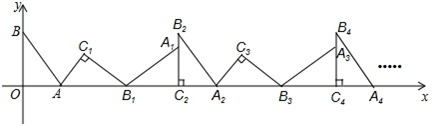
 如图3所示,数轴的一部分被墨水污染,被污染的部分内含有的整数为-2,-1,0,1.
如图3所示,数轴的一部分被墨水污染,被污染的部分内含有的整数为-2,-1,0,1.