题目内容
5.如图1,AB、CD是⊙O的弦,AB⊥CD,垂足为F,E是AB上一点,AE=CE.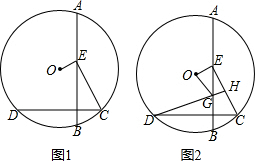
(1)延长OE与弧AC相交于点M,求证:点M是弧AC中点;
(2)如图2,点G在AB上,连接DG,OG,延长DG,与EC相交于点H,若DG=AG.求证:∠DHC=2∠EOG;
(3)在(2)的条件下,若∠EOG=60°,CH=2,AB=8.求CD的长.
分析 (1)如图1中,连接OA、OC、AC,由OA=OC,AE=CE可知OE垂直平分线段AC,所以根据垂径定理可知点M是弧AC的中点;
(2)如图2中,连接OA、AC、OC、OD,OC与DH交于点M.只要证明∠DHC=∠DOC,∠DHC=2∠EOG,即可解决问题.
(3)如图3中,延长DH交⊙O于M,延长CE交⊙O于P,连接CM,DP,OD,OC,OH,作OQ⊥AB于Q,OK⊥DM于K,ON⊥DC于N.首先证明△CHM,△DHP是等边三角形,根据弦心距相等弦相等由OQ=OK推出AB=DM,在Rt△OKH中,由∠OHK=30°,KH=2,求出OK,在Rt△ODN中,由∠DON=60°,DN=OD•sin60°,求出DN即可解决问题.
解答 解:(1)连接OA,OC,AC,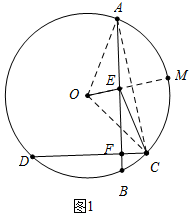
∵OA=OC,AE=CE,
∴点O,E在线段AC的垂直平分线上,
∴OM⊥AC,
∴点M是弧AC中点;
(2)如图2中,连接OA、AC、OC、OD,OC与DH交于点M.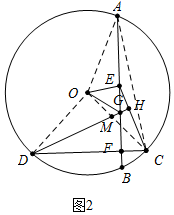
∵OE=OE,OA=OC,AE=EC,
∴△OEA≌△OEC,
∴∠OAE=∠OCE,∠AOE=∠EOC,
∵OG=OG,OA=OD,AG=DG,
∴△OGA≌△OGD,
∴∠OAG=∠ODG=∠OCE,∠GOA=∠GOD,
∵∠OMD=∠HMC,
∴∠DHC=∠DOC,
∵∠EOG=∠GOA-∠EOA=$\frac{1}{2}$(∠GOA+∠GOD-$\frac{1}{2}$AOC)=$\frac{1}{2}$(∠DOC+∠AOC)-$\frac{1}{2}$∠AOC=$\frac{1}{2}$∠DOC,
∴∠DHC=2∠EOG.
(3)如图3中,延长DH交⊙O于M,延长CE交⊙O于P,连接CM,DP,OD,OC,OH,作OQ⊥AB于Q,OK⊥DM于K,ON⊥DC于N.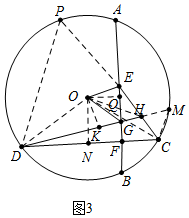
由(2)可知∠OGA=∠OGD,
∵OQ⊥GA,OK⊥GD,
∴OQ=OK,
∴AB=DM=8,
∵∠DHC=∠DOC=2∠EOG,∠EOG=60°,
∴∠DOC=120°,
∴∠M=∠MHC=60°,
∴△HCM是等边三角形,
∴CH=HM=CM=2,
∵∠P=∠PHD=60°,
∴△PHD是等边三角形,
∴DH=DM--HM=6,DK=KM=4,KH=2,
在Rt△OKH中,∵∠OHK=30°,KH=2,
∴OK=$\frac{2\sqrt{3}}{3}$,
∴OD=$\sqrt{D{K}^{2}+O{K}^{2}}$=$\frac{2\sqrt{39}}{3}$,
在Rt△ODN中,∵∠DON=60°,
∴DN=OD•sin60°=$\sqrt{13}$,
∵ON⊥DC,
∴CD=2DN=2$\sqrt{13}$.
点评 本题考查圆的综合问题、垂径定理、勾股定理、垂直平分线的判定、等边三角形的判定、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | x2+2x-3=x(x+2)-3 | B. | 6p(p+q)-4q(p+q)=(p+q)(6p-4q) | ||
| C. | a2-2a+1=(a-1)2 | D. | 4x2-9=(4x+3)(4x-3) |
 已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )| A. | a<b | B. | a+b>0 | C. | ab<0 | D. | b-a>0 |
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
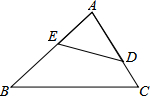 如图,下列条件不能判定△ABC与△ADE相似的是( )
如图,下列条件不能判定△ABC与△ADE相似的是( )| A. | $\frac{AE}{AC}=\frac{AD}{AB}$ | B. | ∠B=∠ADE | C. | ∠C=∠AED | D. | $\frac{AE}{AC}=\frac{DE}{BC}$ |
 如图所示,俯视图上标有正方体的个数,请你画出从正面和左面看到的这个几何体的形状图.
如图所示,俯视图上标有正方体的个数,请你画出从正面和左面看到的这个几何体的形状图.