题目内容
4.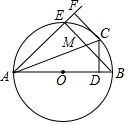 如图,AB为⊙O的直径,点C是⊙O上的一点,CD⊥AB,垂足为点D,CF⊥AF,且CF=CD,AF交⊙O于点E,BE交AC于点M.
如图,AB为⊙O的直径,点C是⊙O上的一点,CD⊥AB,垂足为点D,CF⊥AF,且CF=CD,AF交⊙O于点E,BE交AC于点M.(1)求证:CF是⊙O的切线;
(2)试探究CD、AF、BD之间的数量关系;并证明你的结论.
(3)若AB=6,cos∠BCD=$\frac{5}{6}$,求AM的长.
分析 (1)连接OC根据角平分线性质得出∠FAC=∠BAC,根据垂径定理得出OC⊥BE,求出∠CFE=∠FEB=∠ENC=90°,求出∠OCF=90°,根据切线判定推出即可.
(2)由“HL“定理证得Rt△ACF≌Rt△ACD,得到AF=AD,由射影定理即可证得结论;
(3)求出AC和BC,证△BCM和△CAB相似,得出比例式,求出CM,即可得出答案.
解答 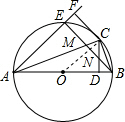 (1)证明:
(1)证明:
连接OC交BE于N,
∵CF⊥AF,CD⊥AB,CF=CD,
∴∠FAC=∠DAC,
∴$\widehat{CE}$=$\widehat{BC}$,
∴OC⊥BE,
∵AB是直径,
∴∠EFC=∠FEN=∠ENC=90°,
∴∠FCO=360°-90°-90°-90°=90°,
即OC⊥CF,
∵OC为半径,
∴CF是⊙O的切线.
(2)CD2=AF•BD;
证明:在Rt△ACF和Rt△ACD中$\left\{\begin{array}{l}{CF=CD}\\{AC=AC}\end{array}\right.$,
∴Rt△ACF≌Rt△ACD,
∴AF=AD,
∵AB为⊙O的直径,
∴∠ACB=90°,
由射影定理得:CD2=AD•BD,
∴CD2=AF•BD;
(3)解:∵AB是直径,CD⊥AB,
∴∠ACB=∠CDB=90°,
∴∠CAB+∠CBA=90°,∠BCD+∠CBA=90°,
∴∠BCD=∠CAB,
∵AB=6,cos∠BCD=$\frac{5}{6}$,
∴cos∠CAB=$\frac{AC}{AB}$=$\frac{5}{6}$,
∴AC=5,
由勾股定理得:BC=$\sqrt{{6}^{2}-{5}^{2}}$=$\sqrt{11}$,
∵弧CE=弧BC,
∴∠EAC=∠CBE=∠CAB,
即∠CBM=∠CAB,
∵∠ACB=∠ACB,
∴△CAB∽△CBM,
∴$\frac{BC}{AC}$=$\frac{CM}{BC}$,
∵BC=$\sqrt{11}$,AC=5,
∴CM=$\frac{11}{5}$,
∴AM=AC-CM=5-$\frac{11}{5}$=$\frac{14}{5}$.
点评 本题考查了切线的判定,角平分线性质,相似三角形的性质和判定,垂径定理,圆周角定理的应用,主要考查学生的推理能力,正确作出辅助线是解题的关键.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | 5y2•4x2y=9x2y3 | B. | (-2x3ynz)•(-4xn+1yn+3)=8xn+1y2n+3 | ||
| C. | 2a2bc÷$\frac{1}{2}$a2b=4c | D. | $\frac{1}{5}$a2b3c2÷(-5abc)2=5b |
| A. | a-1<b-1 | B. | 2a<2b | C. | a-b<0 | D. | -a<-b |
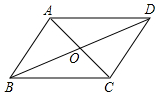 如图,平行四边形ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,平行四边形ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )| A. | 26 | B. | 20 | C. | 17 | D. | 13 |
 如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.
如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.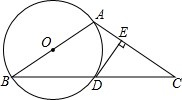 如图,已知△ABC中,AB=AC,以AB为直径的⊙O交 BC于点D,过D作DE⊥AC于E.
如图,已知△ABC中,AB=AC,以AB为直径的⊙O交 BC于点D,过D作DE⊥AC于E.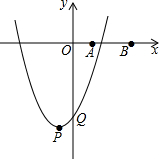 如图,在平面直角坐标系中,点A、B的坐标分别为A(1,0)、B(3,0).抛物线y=x2-2mx+m2-4的顶点为P,与y轴的交点为Q.
如图,在平面直角坐标系中,点A、B的坐标分别为A(1,0)、B(3,0).抛物线y=x2-2mx+m2-4的顶点为P,与y轴的交点为Q.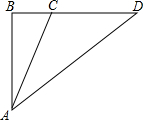 如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?
如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?