题目内容
5.图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形.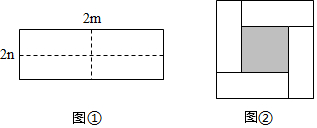
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:S小正方形=(m+n)2-4mn;
方法二:S小正方形=(m-n)2;
(2)(m+n)2,(m-n)2,mn这三个代数式之间的等量关系为(m+n)2-4mn=(m-n)2
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求x-y的值.
分析 (1)观察图形可确定:方法一,大正方形的面积为(m+n)2,四个小长方形的面积为4mn,中间阴影部分的面积为S=(m+n)2-4mn;
方法二,图2中阴影部分为正方形,其边长为m-n,所以其面积为(m-n)2.
(2)观察图形可确定,大正方形的面积减去四个小长方形的面积等于中间阴影部分的面积,即(m+n)2-4mn=(m-n)2.
(3)根据(2)的关系式代入计算即可求解.
解答 解:(1)方法一:S小正方形=(m+n)2-4mn.
方法二:S小正方形=(m-n)2.
(2)(m+n)2,(m-n)2,mn这三个代数式之间的等量关系为(m+n)2-4mn=(m-n)2.
(3)∵x+y=9,xy=14,
∴x-y=±$\sqrt{(x+y)^{2}-4xy}$=±5.
故答案为:(m+n)2-4mn,(m-n)2;(m+n)2-4mn=(m-n)2.
点评 本题是完全平方式的实际应用,完全平方式经常与正方形的面积公式和长方形的面积公式联系在一起,要学会观察图形.

练习册系列答案
相关题目
20. 如图,∠1=∠2,下列选项中不能证明△ABC∽△ADE的是( )
如图,∠1=∠2,下列选项中不能证明△ABC∽△ADE的是( )
 如图,∠1=∠2,下列选项中不能证明△ABC∽△ADE的是( )
如图,∠1=∠2,下列选项中不能证明△ABC∽△ADE的是( )| A. | ∠B=∠D | B. | ∠C=∠E | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{AD}{AB}$=$\frac{DE}{BC}$ |
10.要想了解10万名考生的数学成绩,从中抽取了2000名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这2000名考生是总体的一个样本 | B. | 每位考生的数学成绩是个体 | ||
| C. | 10万名考生是个体 | D. | 10万名考生是总体 |
17.下列计算正确的是( )
| A. | 2$\sqrt{3}$+3$\sqrt{3}$=6$\sqrt{3}$ | B. | 5$\sqrt{5}$-2$\sqrt{3}$=3$\sqrt{2}$ | C. | $\sqrt{3}$÷$\sqrt{2}$=$\frac{\sqrt{6}}{2}$ | D. | ($\sqrt{5}$)-2=$\frac{2}{5}$ |
14.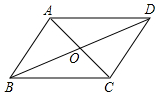 如图,平行四边形ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,平行四边形ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
 如图,平行四边形ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,平行四边形ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )| A. | 26 | B. | 20 | C. | 17 | D. | 13 |
15.四边形的内角和等于x°,五边形的外角和等于y°,则下列关系成立的是( )
| A. | x=y | B. | x=2y | C. | x=y+180 | D. | y=x+180 |
 如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.
如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.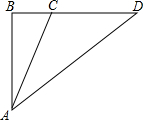 如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?
如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?