题目内容
9.抛物线y=x2-(m+1)x+9与x轴只有一个交点,则m的值为-7或5.分析 利用抛物线与x轴只有一个交点,令y=x2-(m+1)x+9=0,根据b2-4ac=0进而求出m的值即可.
解答 解:∵抛物线y=x2-(m+1)x+9与x轴只有一个交点,
∴令y=x2-(m+1)x+9=0,
∴b2-4ac=(m+1)2-4×9=0,
解得:m=-7或5,
故答案为:-7或5.
点评 本题主要考查了抛物线与x轴交点的知识,正确把握抛物线与x轴交点个数确定方法是解题关键,此题难度不大.

练习册系列答案
相关题目
14. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③a-b>0;④m>2,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③a-b>0;④m>2,其中正确结论的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③a-b>0;④m>2,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③a-b>0;④m>2,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.下列事件中,属于随机事件的是( )
| A. | 通常温度降到0℃以下,纯净的水结冰 | |
| B. | 随意翻到一本书的某页,这页的页码是奇数 | |
| C. | 掷一枚普通正方体骰子,向上的一面是7点 | |
| D. | 测量某天的最低气温,结果为-150℃ |
18.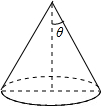 如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )
如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )
 如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )
如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )| A. | $\frac{5}{12}$ | B. | $\frac{5}{13}$ | C. | $\frac{10}{13}$ | D. | $\frac{12}{13}$ |
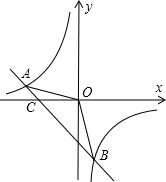 如图,已知点A(一8,n),B(3,-8)是一次函数y=kx+b的图象和反比例函数$y=\frac{m}{x}$图象的两个交点.
如图,已知点A(一8,n),B(3,-8)是一次函数y=kx+b的图象和反比例函数$y=\frac{m}{x}$图象的两个交点.