题目内容
20.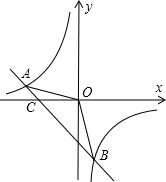 如图,已知点A(一8,n),B(3,-8)是一次函数y=kx+b的图象和反比例函数$y=\frac{m}{x}$图象的两个交点.
如图,已知点A(一8,n),B(3,-8)是一次函数y=kx+b的图象和反比例函数$y=\frac{m}{x}$图象的两个交点.(1)求反比例函数的解析式;
(2)求A点的坐标;
(3)请直接写出方程$kx+b-\frac{m}{x}=0$的解.
分析 (1)由B点在在反比例函数$y=\frac{m}{x}$的图象上,可求出m,从而求出函数解析式;
(2)由A点在在反比例函数$y=\frac{m}{x}$的图象上,把A的坐标代入(1)求得的解析式即可求得n的值,从而求得A的坐标;
(3)观察函数的图象,结合A、B的坐标即可求出方程$kx+b-\frac{m}{x}=0$的解.
解答 解:(1)∵B(3,-8)在反比例函数$y=\frac{m}{x}$的图象上,
∴m=-24,
∴反比例函数的解析式为y=-$\frac{24}{x}$.
(2)∵A(一8,n)在反比例函数y=-$\frac{24}{x}$的图象上,
∴n=-$\frac{24}{-8}$=3,
∵A(一8,3).
(3)∵A(一8,3),B(3,-8),
∴方程$kx+b-\frac{m}{x}=0$的解为x=3或-8.
点评 此题考查一次函数和反比例函数的性质及图象,考查用待定系数法求函数的解析式,还间接考查根据交点坐标,从而来解方程.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
15.在△ABC和△A′B′C′中,∠B=∠B′,下列条件不能判断这两个三角形相似的是( )
| A. | ∠A=∠C′ | B. | ∠A=∠A′ | C. | $\frac{AB}{BC}=\frac{A′B′}{B′C′}$ | D. | $\frac{AB}{AC}=\frac{A′B′}{A′C′}$ |
10.在祁家河初中组织的演讲比赛中,七、八年级各有两名同学进入决赛,九年级有一名同学进入决赛,那么九年级同学获得第一名或第二名的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
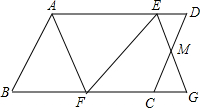 已知,如图,在?ABCD中,AB=8cm,BC=12cm,点E,F分别是边BC,AD上的动点,点E与点F同时出发,点E从点B开始以2cm/s的速度向点C运动,点F从点D开始以1cm/s的速度向点A运动,当其中一个点到达终点时,另一个点也立即停止运动,设运动时间为t秒,若M为CD的中点,连接FM并延长,交直线BC于点G.
已知,如图,在?ABCD中,AB=8cm,BC=12cm,点E,F分别是边BC,AD上的动点,点E与点F同时出发,点E从点B开始以2cm/s的速度向点C运动,点F从点D开始以1cm/s的速度向点A运动,当其中一个点到达终点时,另一个点也立即停止运动,设运动时间为t秒,若M为CD的中点,连接FM并延长,交直线BC于点G.
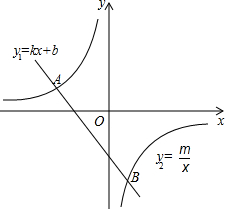 如图,已知A(-2,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$(m≠0)的图象的两个交点,则当0<y1≤y2时,x的取值范围是-2≤x<-1.
如图,已知A(-2,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$(m≠0)的图象的两个交点,则当0<y1≤y2时,x的取值范围是-2≤x<-1.