题目内容
18.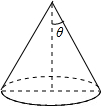 如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )
如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )| A. | $\frac{5}{12}$ | B. | $\frac{5}{13}$ | C. | $\frac{10}{13}$ | D. | $\frac{12}{13}$ |
分析 圆锥的侧面积=π×底面半径×母线长,把相应数值代入即可求得圆锥的母线长.根据余弦函数定义求解.
解答 解:设圆锥的母线长为R,由题意得65π=π×5×R,
解得R=13,
由勾股定理圆锥的高为$\sqrt{1{3}^{2}-{5}^{2}}$=12.
∴cosθ=$\frac{12}{13}$,
故选D.
点评 本题考查圆锥侧面积公式的运用,注意一个角的正弦值等于这个角的对比与斜边之比.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
3. 已知y=ax2+bx+c的图象如图所示,则y=ax-bc的图象一定不经过( )
已知y=ax2+bx+c的图象如图所示,则y=ax-bc的图象一定不经过( )
 已知y=ax2+bx+c的图象如图所示,则y=ax-bc的图象一定不经过( )
已知y=ax2+bx+c的图象如图所示,则y=ax-bc的图象一定不经过( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.在祁家河初中组织的演讲比赛中,七、八年级各有两名同学进入决赛,九年级有一名同学进入决赛,那么九年级同学获得第一名或第二名的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
 如图,?ABCD的对角线AC、BD相交于点O,点E、F分别是线段AO、BO的中点,若EF=3,△OAB的周长是14,则AC+BD=16.
如图,?ABCD的对角线AC、BD相交于点O,点E、F分别是线段AO、BO的中点,若EF=3,△OAB的周长是14,则AC+BD=16. 如图,已知AB∥CD,∠BAF=∠FED=21°,∠CDE=17°,则∠AFC=59°.
如图,已知AB∥CD,∠BAF=∠FED=21°,∠CDE=17°,则∠AFC=59°.